题目内容
在 中,已知角
中,已知角 ,
, ,
,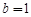 ,解此三角形。
,解此三角形。
 中,已知角
中,已知角 ,
, ,
,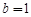 ,解此三角形。
,解此三角形。 ,
, ,
,
试题分析:)由正弦定理得,
 ,
, 3分
3分 ,
,
所以,由正弦定理得
 8分
8分点评:本题主要考查了正弦定理的运用,以及两角和差的三角公式的运用,属于基础题

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
题目内容
 中,已知角
中,已知角 ,
, ,
,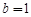 ,解此三角形。
,解此三角形。 ,
, ,
,
 ,
, 3分
3分 ,
,
 8分
8分
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案