题目内容
已知 求
求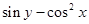 的最大值
的最大值
 求
求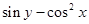 的最大值
的最大值
【错解分析】此题学生都能通过条件
 将问题转化为关于
将问题转化为关于 的函数,进而利用换元的思想令
的函数,进而利用换元的思想令 将问题变为关于t的二次函数最值求解。但极易忽略换元前后变量的等价性而造成错解,
将问题变为关于t的二次函数最值求解。但极易忽略换元前后变量的等价性而造成错解,【正解】由已知条件有
 且
且 (结合
(结合 )
)得
 ,而
,而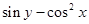 =
=
 =
=
令
 则原式=
则原式=
根据二次函数配方得:当
 即
即 时,原式取得最大值
时,原式取得最大值 。
。【点评】“知识”是基础,“方法”是手段,“思想”是深化,提高数学素质的核心就是提高学生对数学思想方法的认识和运用,数学素质的综合体现就是“能力”,解数学题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这叫换元法。换元的实质是转化,关键是构造元和设元,理论依据是等量代换,目的是变换研究对象,将问题移至新对象的知识背景中去研究,从而使非标准型问题标准化、复杂问题简单化,变得容易处理。换元法又称辅助元素法、变量代换法。通过引进新的变量,可以把分散的条件联系起来,隐含的条件显露出来,或者把条件与结论联系起来。或者变为熟悉的形式,把复杂的计算和推证简化。

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
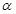 的终边落在射线
的终边落在射线 上,则
上,则 =____________。
=____________。 为偶函数,则
为偶函数,则 可以取的一个值为( )
可以取的一个值为( )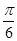

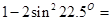 ________.
________.
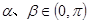 ,且
,且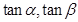 是方程
是方程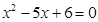 的两根.
的两根.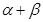 的值. (2)求
的值. (2)求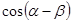 的值.
的值. ,求
,求 的值;
的值; ,求
,求 的值
的值 为第二象限角,
为第二象限角, ,则
,则 ( ).
( ).



 的终边上有一点
的终边上有一点 ,则
,则 的值是.
的值是.


