题目内容
袋里装有除编号不同外没有其它区别的20个球，其编号为n（1≤n≤20，n∈N*）；对于函数f(x)=
x2-5x+
，如果满足f（n）＞n，其中n为袋里球的编号（1≤n≤20，n∈N*），则称该球“超号球”，否则为“保号球”．
（Ⅰ）如果任意取出1球，求该球恰为“超号球”的球概率；
（Ⅱ）（理）如果同时任意取出两个球，记这两球中“超号球”的个数为随机变量ξ，求ξ的分布列及数学期望．
| 1 |
| 3 |
| 65 |
| 3 |
（Ⅰ）如果任意取出1球，求该球恰为“超号球”的球概率；
（Ⅱ）（理）如果同时任意取出两个球，记这两球中“超号球”的个数为随机变量ξ，求ξ的分布列及数学期望．
分析：（Ⅰ）任取1个球，共有20个等可能的结果，由
n2-5n+
＞n，知“超号球”数为11，由此能求出任意取出1球，该球恰为“超号球”的球概率．
（Ⅱ）同时任意取出两个球，重球个数ξ可能的值有0、1、2，由题设条件分别求出P（ξ=0），P（ξ=1）和P（ξ=2），由此能求出ξ的分布列和Eξ．
| 1 |
| 3 |
| 65 |
| 3 |
（Ⅱ）同时任意取出两个球，重球个数ξ可能的值有0、1、2，由题设条件分别求出P（ξ=0），P（ξ=1）和P（ξ=2），由此能求出ξ的分布列和Eξ．
解答：解：（Ⅰ）任取1个球，共有20个等可能的结果，
由
n2-5n+
＞n，
即n2-18n+65＞0，
所以n＜5或n＞13．
∵1≤n≤20，n∈N*，
∴满足条件的n有：1，2，3，4，14，15，16，17，18，19，20，
因此“超号球”数为11，
所以概率为
．
（Ⅱ）同时任意取出两个球，重球个数ξ可能的值有0、1、2，
P（ξ=0）=
=
，
P（ξ=1）=
=
，
P（ξ=2）=
=
．
∴ξ的分布列为：
∴Eξ=0×
+1×
+2×
=
，
∴Eξ=
．
由
| 1 |
| 3 |
| 65 |
| 3 |
即n2-18n+65＞0，
所以n＜5或n＞13．
∵1≤n≤20，n∈N*，
∴满足条件的n有：1，2，3，4，14，15，16，17，18，19，20，
因此“超号球”数为11，
所以概率为
| 11 |
| 20 |
（Ⅱ）同时任意取出两个球，重球个数ξ可能的值有0、1、2，
P（ξ=0）=
| ||
|
| 36 |
| 190 |
P（ξ=1）=
| ||||
|
| 99 |
| 190 |
P（ξ=2）=
| ||
|
| 55 |
| 190 |
∴ξ的分布列为：
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 36 |
| 190 |
| 99 |
| 190 |
| 55 |
| 190 |
| 209 |
| 190 |
∴Eξ=
| 209 |
| 190 |
点评：本题考查离散型随机变量的分布列和数学期望，考查学生的运算能力，考查学生探究研究问题的能力，解题时要认真审题，理解古典概型的特征：试验结果的有限性和每一个试验结果出现的等可能性，体现了化归的重要思想．
练习册系列答案
相关题目
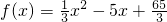，如果满足f（n）＞n，其中n为袋里球的编号（1≤n≤20，n∈N*），则称该球“超号球”，否则为“保号球”．
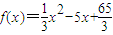，如果满足f（n）＞n，其中n为袋里球的编号（1≤n≤20，n∈N*），则称该球“超号球”，否则为“保号球”．