题目内容
已知两点P(4,-9),Q(-2,3),则直线PQ与y轴的交点分有向线段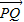 的比为 .
的比为 .
【答案】分析:直线PQ与y轴的交点 的横坐标等于0,由定比分点坐标公式可得 0= ,解得 λ=2,从而得到答案.
,解得 λ=2,从而得到答案.
解答:解:直线PQ与y轴的交点 的横坐标等于0,由定比分点坐标公式可得 0=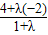 ,
,
解得 λ=2,故直线PQ与y轴的交点分有向线段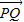 的比为 λ=2,
的比为 λ=2,
故答案为:2.
点评:本题考查定比分点分有向线段成的比的定义,定必分点坐标公式 的应用,得到0=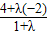 ,是解题的关键.
,是解题的关键.
 ,解得 λ=2,从而得到答案.
,解得 λ=2,从而得到答案.解答:解:直线PQ与y轴的交点 的横坐标等于0,由定比分点坐标公式可得 0=
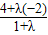 ,
,解得 λ=2,故直线PQ与y轴的交点分有向线段
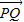 的比为 λ=2,
的比为 λ=2,故答案为:2.
点评:本题考查定比分点分有向线段成的比的定义,定必分点坐标公式 的应用,得到0=
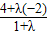 ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目
已知两点P(4,-9),Q(-2,3),则直线PQ与y轴的交点分
所成的比为( )
| PQ |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
 的比为 .
的比为 .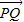 的比为 .
的比为 .