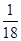题目内容
将一个质地均匀的正方体(六个面上分别标有数字0,1,2,3,4,5)和一个正四面体(四个面分别标有数字1,2,3,4)同时抛掷1次,规定“正方体向上的面上的数字为a,正四面体的三个侧面上的数字之和为b”.设复数为z=a+bi.(1)若集合A={z|z为纯虚数},用列举法表示集合A;
(2)求事件“复数在复平面内对应的点(a,b)满足a2+(b-6)2≤9”的概率.
分析:(1)b的可能取值为1,2,3,4中任取3个数的和,求出b的值进而可求集合A
(2)满足条件的基本事件空间中基本事件的个数为24,设满足“复数在复平面内对应的点(a,b)满足a2+(b-6)2≤9”的事件为B.当a=0时,b=6,7,8,9,当a=1时,b=6,7,8,当a=2时,b=6,7,8,当a=3时,b=6,利用古典概率的计算公式可求
(2)满足条件的基本事件空间中基本事件的个数为24,设满足“复数在复平面内对应的点(a,b)满足a2+(b-6)2≤9”的事件为B.当a=0时,b=6,7,8,9,当a=1时,b=6,7,8,当a=2时,b=6,7,8,当a=3时,b=6,利用古典概率的计算公式可求
解答:解:(1)A={6i,7i,8i,9i}…(4分)
(2)满足条件的基本事件空间中基本事件的个数为24 …(5分)
设满足“复数在复平面内对应的点(a,b)满足a2+(b-6)2≤9”的事件为B.
当a=0时,b=6,7,8,9满足a2+(b-6)2≤9;
当a=1时,b=6,7,8满足a2+(b-6)2≤9;
当a=2时,b=6,7,8满足a2+(b-6)2≤9;
当a=3时,b=6满足a2+(b-6)2≤9; …(10分)
即B:{(0,6),(0,7),(0,8),(0,9),(1,6),(1,7),(1,8),(2,6),(2,7),(2,8),(3,6)}共计11个,
所以:P(B)=
.…(12分)
(2)满足条件的基本事件空间中基本事件的个数为24 …(5分)
设满足“复数在复平面内对应的点(a,b)满足a2+(b-6)2≤9”的事件为B.
当a=0时,b=6,7,8,9满足a2+(b-6)2≤9;
当a=1时,b=6,7,8满足a2+(b-6)2≤9;
当a=2时,b=6,7,8满足a2+(b-6)2≤9;
当a=3时,b=6满足a2+(b-6)2≤9; …(10分)
即B:{(0,6),(0,7),(0,8),(0,9),(1,6),(1,7),(1,8),(2,6),(2,7),(2,8),(3,6)}共计11个,
所以:P(B)=
| 11 |
| 24 |
点评:本题主要考查了古典概率的计算公式的应用,解答(2)的关键是要由a2+(b-6)2≤9要对a的值分类讨论.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 。
。 {
{ 为纯虚数},用列举法表示集合A;
为纯虚数},用列举法表示集合A; ”的概率。
”的概率。 B、
B、 C、
C、 D、
D、