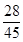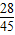题目内容
已知在10件产品中有2件次品,现从中任意抽取2件产品,则至少抽出1件次品的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:由已知中在10件产品中有2件次品,我们可以计算出从中任意抽取2件产品的所有情况数,及满足条件至少抽出1件次品的情况数,代入古典概型概率计算公式,即可得到答案.
解答:解:从10件产品中,任意抽取2件产品,共有
C102=45种情况
其中至少抽出1件次品包括正好抽取一件次品,和抽取两件次品两类
共C81•C21+C22=17情况
故从中任意抽取2件产品,则至少抽出1件次品的概率P=
故选C
C102=45种情况
其中至少抽出1件次品包括正好抽取一件次品,和抽取两件次品两类
共C81•C21+C22=17情况
故从中任意抽取2件产品,则至少抽出1件次品的概率P=
| 17 |
| 45 |
故选C
点评:本题考查的知识点是等可能事件的概率,古典概型概率公式,其中根据已知条件,求出基本事件总数及满足条件的基本事件个数,是解答本题的关键.

练习册系列答案
相关题目
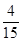 B.
B.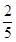 C.
C.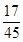 D.
D.