Question

已知：集合A＝{x|－2≤x≤2}，B＝{x|－x≤x≤1}．对应关系f：x→y＝ax.若在f的作用下能够建立从A到B的映射f：A→B，求实数a的取值范围．

Answer 1

解：①当a≥0时，由－2≤x≤2得－2a≤ax≤2a.

若能够建立从A到B的映射．

则[－2a,2a]⊆[－1,1]，

即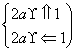，∴0≤a≤.

②当a<0时，集合A中元素的象满足2a≤ax≤－2a，

若能建立从A到B的映射，

则[2a，－2a]⊆[－1,1]，

即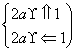∴0>a≥－.

综合①②可知－≤a≤.