题目内容
已知集合A={-1,0,1, 2},B={x|x2-x≤0},则A∩B= .
{0, 1}
解析试题分析:根据题意,由于集合A={-1,0,1, 2},B={x|x2-x≤0},那么由一元二次不等式的解集可知B={x|x2-x≤0}=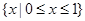 ,故可知A∩B="{0," 1},故答案为{0, 1}
,故可知A∩B="{0," 1},故答案为{0, 1}
考点:交集的运算
点评:解决关键是对于集合B的准确表示,结合一元二次不等式的解集得到,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
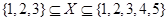 的集合
的集合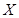 的个数为:
的个数为: 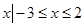 },B={x
},B={x },且A
},且A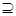 B,实数k的取值范围是 。
B,实数k的取值范围是 。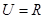 ,集合
,集合 ,则
,则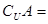
 ,则
,则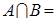 .
.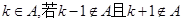 ,则k是A的一个“孤立元”,给定
,则k是A的一个“孤立元”,给定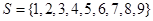 ,由S的3个元素构成的所有集合中,不含“孤立元”的集合共有 个。
,由S的3个元素构成的所有集合中,不含“孤立元”的集合共有 个。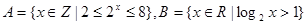 ,则
,则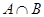 =__________。
=__________。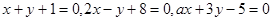 不能围成三角形,则
不能围成三角形,则 的取值集合是 _
的取值集合是 _ 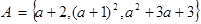 ,若
,若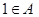 ,则实数
,则实数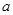 的值为
的值为