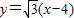题目内容
等边△PQR中,P(0,0)、Q(4,0),且R在第四象限内,则PR和QR所在直线的方程分别为
- A.
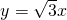
- B.
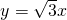 和
和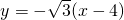
- C.
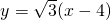
- D.
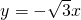 和
和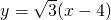
D
分析:由题意可得Q(2,-2 ),进而可得所求直线的斜率,可得直线的方程.
),进而可得所求直线的斜率,可得直线的方程.
解答:由题意可得Q(2,-2 ),
),
故直线PR的斜率为:kPR=- ,
,
故直线PR的方程为:y=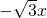 ,
,
而直线QR的斜率为:kQR=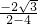 =
= ,
,
以直线QR的方程为:y= (x-4)
(x-4)
故选D
点评:本题考查直线方程的求解,涉及等边三角形的知识,属基础题.
分析:由题意可得Q(2,-2
 ),进而可得所求直线的斜率,可得直线的方程.
),进而可得所求直线的斜率,可得直线的方程.解答:由题意可得Q(2,-2
 ),
),故直线PR的斜率为:kPR=-
 ,
,故直线PR的方程为:y=
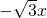 ,
,而直线QR的斜率为:kQR=
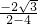 =
= ,
,以直线QR的方程为:y=
 (x-4)
(x-4)故选D
点评:本题考查直线方程的求解,涉及等边三角形的知识,属基础题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
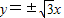
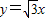 和
和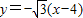
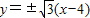
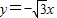 和
和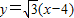
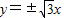
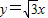 和
和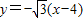
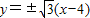
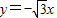 和
和