题目内容
已知定义域为 的函数
的函数 ,如果对任意的
,如果对任意的 ,存在正数
,存在正数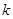 ,有
,有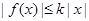 成立,
成立,
则称函数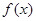 是
是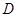 上的“倍约束函数”,已知下列函数:(1)
上的“倍约束函数”,已知下列函数:(1)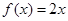 ;(2)
;(2)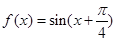
(3)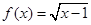 ;(4)
;(4)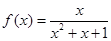 ;其中是“倍约束函数”的是 ( )
;其中是“倍约束函数”的是 ( )
| A.(1)(3)(4) | B.(1)(2) | C.(3)(4) | D.(2)(3)(4) |
A
解析考点:函数的概念及其构成要素.
分析:此题考查的是新定义问题与恒成立问题相结合的综合类问题.在解答时可以逐一排查.
解析:∵对任意x∈D,存在正数k,都有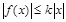 成立∴对任意x∈D,存在正数k,都有k≥
成立∴对任意x∈D,存在正数k,都有k≥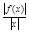 成立.∴对①f(x)=2x,易知存在k=2符合题意;对②当x趋近于0时,则
成立.∴对①f(x)=2x,易知存在k=2符合题意;对②当x趋近于0时,则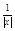 趋近于正无穷大,
趋近于正无穷大,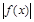 趋近于常数
趋近于常数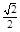 ,所以
,所以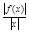 趋近于正无穷大,即不存在k≥
趋近于正无穷大,即不存在k≥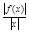 恒成立。
恒成立。
对③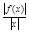 =
=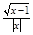 =
=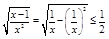 ,从而存在正数k≥
,从而存在正数k≥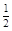 符合题意。
符合题意。
对④有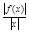 =
=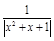 =
=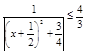 ,从而存在正数k≥
,从而存在正数k≥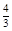 符合题意。故答案为:①③④.
符合题意。故答案为:①③④.
点评:此题考查的是新定义问题与恒成立问题相结合的综合类问题.正确理解题目中给的新定义是解决问题的关健.同时要掌握恒成立问题的解题方法.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
已知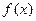 是定义在R上的奇函数,满足
是定义在R上的奇函数,满足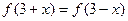 ,且当
,且当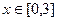 时,
时,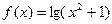 ,则
,则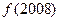 的值是( )
的值是( )
| A.0 | B.1 | C. | D.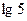 |
同时满足两个条件:①定义域内是减函数 ②定义域内是奇函数的函数是
| A.f(x)=-x|x| | B.f(x)= x3 |
| C.f(x)=sinx | D.f(x)= 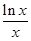 |
设函数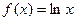 ,当
,当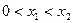 下列结论正确的是( )
下列结论正确的是( )
A. 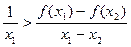 | B. |
C.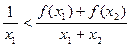 | D.以上都不对。 |
已知函数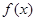 是定义域为
是定义域为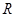 的奇函数,且
的奇函数,且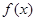 的图象关于直线
的图象关于直线 对称,那么下列式子中对任意
对称,那么下列式子中对任意 恒成立的是
恒成立的是
A.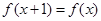 |
B. |
C.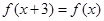 |
D.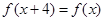 |
设函数f(x)=x|x|+bx+c,给出下列四个命题:
①c=0时,f(x)是奇函数 ②b=0,c>0时,方程f(x)=0只有一个实根
③f(x)的图象关于(0,c)对称 ④方程f(x)=0至多两个实根
其中正确的命题是( )
| A.①④ | B.①③ | C.①②③ | D.①②④ |
已知f(2x+1)是偶函数,则函数f(2x)图像的对称轴为( )
| A.x=1 | B. | C.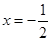 | D.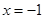 |
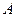 是单位圆上的一定点,动点
是单位圆上的一定点,动点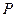 从点
从点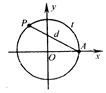
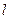 ,弦
,弦 的长为
的长为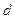 ,则函数
,则函数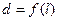 的图像大致是
的图像大致是