题目内容
设复数z满足z·(1－i)＝3－i，i为虚数单位，则z＝( )
| A．1＋2i | B．1－2i |
| C．2＋i | D．2－i |
C
解析
练习册系列答案
名校课堂系列答案
相关题目
已知复数
，则（ ）
A． | B．z的实部为1 | C．z的虚部为﹣1 | D．z的共轭复数为1+i |
复数
（i为虚数单位）的共轭复数在复平面上的对应点位于
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
在复平面内，复数
对应的点位于（ ）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
已知
是虚数单位，若
，则实数
的值为（ ）
A． | B． | C． | D． |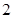
已知z是纯虚数，
是实数，那么z等于 ( )．
| A．2i | B．i | C．－i | D．－2i |
设0<θ<
,a∈R,(a+
i)(1-i)=cosθ+i,则θ的值为( )
A． π | B． π | C． | D． |
若复数z＝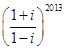
，则ln |z|＝( )
| A．－2 | B．0 | C．1 | D．4 |
复数z＝
，则复数z＋1在复平面上对应的点位于( )．
| A．第一象限 | B．第二象限 |
| C．第三象限 | D．第四象限 |