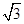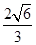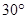题目内容
在棱长均为2的正四棱锥P-ABCD中,点E为PC的中点,则下列命题正确的是( )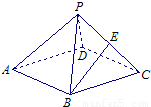
A.BE∥平面PAD,且BE到平面PAD的距离为
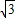
B.BE∥平面PAD,且BE到平面PAD的距离为

C.BE与平面PAD不平行,且BE与平面PAD所成的角大于30°
D.BE与平面PAD不平行,且BE与平面PAD所成的角小于30°
【答案】分析:连接AC,BD,交点为O,以O为坐标原点,OC,OD,OP方向分别x,y,z轴正方向建立空间坐标系,分别求出直线BE的方向向量与平面PAD的法向量,代入向量夹角公式,求出BE与平面PAD夹角的正弦值,再由正弦函数的单调性,即可得到答案.
解答:解:连接AC,BD,交点为O,以O为坐标原点,OC,OD,OP方向分别x,y,z轴正方向建立空间坐标系
由正四棱锥P-ABCD的棱长均为2,点E为PC的中点,
则O(0,0,0),A(-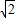 ,0,0),B(0,-
,0,0),B(0,-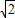 ,0),C(
,0),C(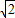 ,0,0),D(0,
,0,0),D(0,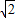 ,0),P(0,0,
,0),P(0,0,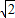 ),E(
),E(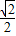 ,0,
,0,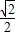 )
)
则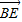 =(
=(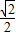 ,
,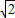 ,
,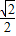 ),
),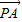 =(-
=(-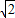 ,0,-
,0,-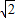 ),
),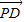 =(0,
=(0,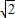 ,-
,-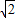 ),
),
设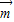 =(x,y,z)是平面PAD的一个法向量,则
=(x,y,z)是平面PAD的一个法向量,则 ⊥
⊥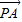 ,且
,且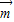 ⊥
⊥
即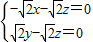 ,令x=1
,令x=1
则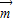 =(1,-1,-1)是平面PAD的一个法向量,
=(1,-1,-1)是平面PAD的一个法向量,
设BE与平面PAD所成的角为θ
则sinθ=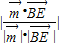 =
=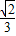 <
<
故BE与平面PAD不平行,且BE与平面PAD所成的角小于30°
故选D
点评:本题考查的知识点是直线与平面所成的角,其中建立适当的空间坐标系,将直线与平面的夹角问题转化为向量夹角问题是解答本题的关键.
解答:解:连接AC,BD,交点为O,以O为坐标原点,OC,OD,OP方向分别x,y,z轴正方向建立空间坐标系
由正四棱锥P-ABCD的棱长均为2,点E为PC的中点,
则O(0,0,0),A(-
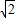 ,0,0),B(0,-
,0,0),B(0,-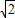 ,0),C(
,0),C(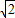 ,0,0),D(0,
,0,0),D(0,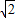 ,0),P(0,0,
,0),P(0,0,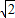 ),E(
),E(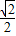 ,0,
,0,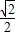 )
)则
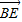 =(
=(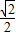 ,
,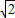 ,
,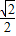 ),
),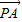 =(-
=(-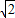 ,0,-
,0,-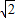 ),
),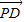 =(0,
=(0,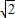 ,-
,-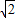 ),
),设
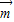 =(x,y,z)是平面PAD的一个法向量,则
=(x,y,z)是平面PAD的一个法向量,则 ⊥
⊥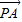 ,且
,且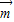 ⊥
⊥
即
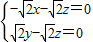 ,令x=1
,令x=1则
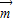 =(1,-1,-1)是平面PAD的一个法向量,
=(1,-1,-1)是平面PAD的一个法向量,设BE与平面PAD所成的角为θ
则sinθ=
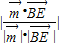 =
=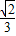 <
<
故BE与平面PAD不平行,且BE与平面PAD所成的角小于30°
故选D
点评:本题考查的知识点是直线与平面所成的角,其中建立适当的空间坐标系,将直线与平面的夹角问题转化为向量夹角问题是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
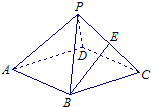 在棱长均为2的正四棱锥P-ABCD中,点E为PC的中点,则下列命题正确的是( )
在棱长均为2的正四棱锥P-ABCD中,点E为PC的中点,则下列命题正确的是( )A、BE∥平面PAD,且BE到平面PAD的距离为
| ||||
B、BE∥平面PAD,且BE到平面PAD的距离为
| ||||
| C、BE与平面PAD不平行,且BE与平面PAD所成的角大于30° | ||||
| D、BE与平面PAD不平行,且BE与平面PAD所成的角小于30° |
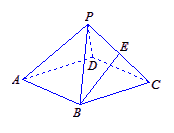
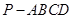 中,点
中,点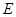 为
为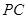 中点,则下列命题正确的是( )
中点,则下列命题正确的是( )
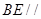 面
面 ,且直线
,且直线 到面
到面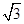

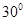
 中,点E为PC的中点,则下列命题正确的是( )(正四棱锥即底面为正方形,四条侧棱长相等,顶点在底面上的射影为底面的中心的四棱锥)
中,点E为PC的中点,则下列命题正确的是( )(正四棱锥即底面为正方形,四条侧棱长相等,顶点在底面上的射影为底面的中心的四棱锥)
 ,且直线BE到面PAD的距离为
,且直线BE到面PAD的距离为

 ,且直线BE与面PAD所成的角大于
,且直线BE与面PAD所成的角大于
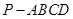 中,点
中,点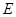 为
为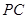 的中点,则下列命题正确的是( )
的中点,则下列命题正确的是( )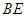 ∥平面
∥平面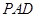 ,且
,且