题目内容
唐徕回中在校际篮球联赛中高三年级代表队中两名队员8场投篮及命中情况记录如下:
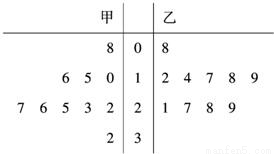
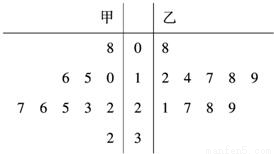
(1)试用茎叶图表示甲、乙两队员投中的次数,并计算甲、乙两队员投中次数的平均数和方差.
(参考公式:s2=
[(x1-
)2+…+(xn-
)2])
(2)设乙队员投球次数为x,投中为y,根据上表,利用统计中的最小二乘法原理建立的回归方程为
=
x+
,其中
=0.44,若乙队员某场比赛中投球28次,估计投中了多少次.
| 场次 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 |
| 甲投球次数 | 30 | 21 | 19 | 22 | 16 | 14 | 17 | 20 |
| 甲投中次数 | 18 | 12 | 8 | 14 | 12 | 10 | 9 | 13 |
| 乙投球次数 | 26 | 18 | 23 | 20 | 24 | 20 | 16 | 19 |
| 乙投中次数 | 14 | 12 | 13 | 13 | 16 | 12 | 9 | 15 |
(参考公式:s2=
| 1 |
| n |
. |
| x |
. |
| x |
(2)设乙队员投球次数为x,投中为y,根据上表,利用统计中的最小二乘法原理建立的回归方程为
| ? |
| y |
| ? |
| b |
| ? |
| a |
| ? |
| b |
分析:(1)画出茎叶图,中间的茎为十位上的数字,叶是数字的个位.把数据按照从小到大的顺序排列以后,利用公式求出甲和乙的平均数和方差.
(2)由(1)求出横标和纵标的平均数,写出样本中心点,把样本中心点代入线性回归方程,得到关于a的方程,解方程求出a,最后将x=28代入求出相应的y即可.
(2)由(1)求出横标和纵标的平均数,写出样本中心点,把样本中心点代入线性回归方程,得到关于a的方程,解方程求出a,最后将x=28代入求出相应的y即可.
解答:解:(1)茎叶图如图,中间的茎为十位上的数字.
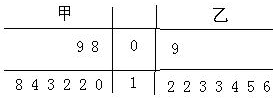
∴
=12,
=13,s
=8.75,s
=4.
(2)由(1)得这组数据的样本中心点是(20.75,13)
把样本中心点代入回归直线方程
=
x+
,其中
=0.44,得a=13-0.44×20.75=3.87,
∴回归直线方程为
=0.44x+3.87,
当x=28时,
=16.19,
故估计投中了19次.

∴
. |
| x甲 |
. |
| x乙 |
2 甲 |
2 乙 |
(2)由(1)得这组数据的样本中心点是(20.75,13)
把样本中心点代入回归直线方程
| ? |
| y |
| ? |
| b |
| ? |
| a |
| ? |
| b |
∴回归直线方程为
 |
| y |
当x=28时,
 |
| y |
故估计投中了19次.
点评:本题考查茎叶图的画法,考查数据的几个常见的量,考查线性回归方程,解题的关键是线性回归直线一定过样本中心点,这是求解线性回归方程的步骤之一.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
唐徕回中在校际篮球联赛中高三年级代表队中两名队员8场投篮及命中情况记录如下:
(1)试用茎叶图表示甲、乙两队员投中的次数,并计算甲、乙两队员投中次数的平均数和方差.
(参考公式: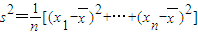 )
)
(2)设乙队员投球次数为x,投中为y,根据上表,利用统计中的最小二乘法原理建立的回归方程为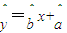 ,其中
,其中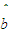 =0.44,若乙队员某场比赛中投球28次,估计投中了多少次.
=0.44,若乙队员某场比赛中投球28次,估计投中了多少次.
| 场次 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 |
| 甲投球次数 | 30 | 21 | 19 | 22 | 16 | 14 | 17 | 20 |
| 甲投中次数 | 18 | 12 | 8 | 14 | 12 | 10 | 9 | 13 |
| 乙投球次数 | 26 | 18 | 23 | 20 | 24 | 20 | 16 | 19 |
| 乙投中次数 | 14 | 12 | 13 | 13 | 16 | 12 | 9 | 15 |
(参考公式:
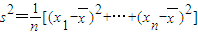 )
)(2)设乙队员投球次数为x,投中为y,根据上表,利用统计中的最小二乘法原理建立的回归方程为
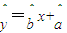 ,其中
,其中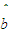 =0.44,若乙队员某场比赛中投球28次,估计投中了多少次.
=0.44,若乙队员某场比赛中投球28次,估计投中了多少次.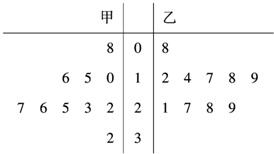 12、如图是CBA篮球联赛中,甲乙两名运动员某赛季一些场次得分的茎叶图,则平均得分高的运动员是
12、如图是CBA篮球联赛中,甲乙两名运动员某赛季一些场次得分的茎叶图,则平均得分高的运动员是