题目内容
已知z1，z2为共轭复数，且z1z2+（z1+z2）i=4-2i．求复数z1及它的模|z2|．
【答案】分析：设z1=a+bi，则z2=a-bi．利用复数的运算法则由z1z2+（z1+z2）i=4-2i，得到（a2+b2）+2ai=4-2i，再由复数相等的概念能求出a和b，从而得到复数z1及它的模|z2|．
解答：解：设z1=a+bi，则z2=a-bi．
∵z1z2+（z1+z2）i=4-2i，
∴（a2+b2）+2ai=4-2i，
∴
，
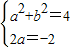解得
，
故，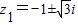
，
从而，|z2|=2．
点评：本题考查复数的模的求法和复数的求法，是基础题．解题时要熟练掌握复数的运算法则，灵活运用复数相等的充要条件进行解题．
解答：解：设z1=a+bi，则z2=a-bi．
∵z1z2+（z1+z2）i=4-2i，
∴（a2+b2）+2ai=4-2i，
∴
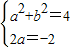，解得
，故，
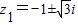，从而，|z2|=2．
点评：本题考查复数的模的求法和复数的求法，是基础题．解题时要熟练掌握复数的运算法则，灵活运用复数相等的充要条件进行解题．
练习册系列答案
高中必刷题系列答案
相关题目
.求复数z1及它的模| z2|．