题目内容
在算式“1×口+4×口=30”的两个口中,分别填入两个自然数,使它们的倒数之和最小,则这两个数的和为________.
15
解析试题分析:先设出两个□,然后利用代入消元法表示出其倒数和,由于该倒数和的形式中分母次数高于分子,则求其倒数的最大值,这与原倒数和的最小值是一致的;最终把代数式转化为x+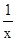 +a(x>0)的形式,利用基本不等式求最值,则由取最值的条件即可解决问题。
+a(x>0)的形式,利用基本不等式求最值,则由取最值的条件即可解决问题。
设1×m+4n=30,m、n∈N+,则m=30-4n,其中1≤n≤7,那么所求的即为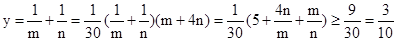 ,那么当且仅当m=2n,解得n=5,m=10,故m+n=15,故答案为15.
,那么当且仅当m=2n,解得n=5,m=10,故m+n=15,故答案为15.
考点:本试题主要考查了代数式向形如x+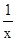 +a(x>0,a为常数)的代数式的转化方法,注意分子次数必须高于分母次数;同时考查基本不等式的运用条件,特别是取等号时的条件.该题代数运较为繁琐,运算量较大,属于难题.
+a(x>0,a为常数)的代数式的转化方法,注意分子次数必须高于分母次数;同时考查基本不等式的运用条件,特别是取等号时的条件.该题代数运较为繁琐,运算量较大,属于难题.
点评:解决该试题的关键是能够构造均值不等式的特征,结合不等式的一正二定三相等的思想来求解最值。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
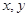 满足
满足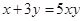 ,则
,则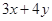 的最小值是____ __
的最小值是____ __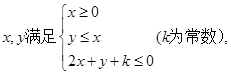 若
若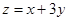 的最大值为8,则k=_____
的最大值为8,则k=_____ ,则
,则 的最小值是
的最小值是 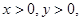 且
且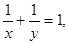 若
若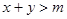 恒成立,则实数m的取值范围是_________.
恒成立,则实数m的取值范围是_________. ,则
,则 的最小值为 ;
的最小值为 ;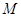 是
是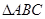 内的一点,且
内的一点,且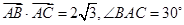 ,若
,若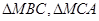 和
和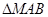 的面积分别为
的面积分别为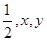 ,则
,则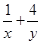 的最小值是 。
的最小值是 。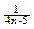 的最小值是___________
的最小值是___________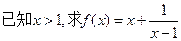 的最小值为
的最小值为