题目内容
设直线y=kx与椭圆 相交于A、B两点,分别过A、B向x轴作垂线,若垂足恰为椭圆的两个焦点,则k等于
相交于A、B两点,分别过A、B向x轴作垂线,若垂足恰为椭圆的两个焦点,则k等于
- A.

- B.

- C.

- D.±2
A
分析:将直线方程与椭圆方程联立,得(3+4k2)x2=12.分别过A、B向x轴作垂线,垂足恰为椭圆的两个焦点,说明A,B的横坐标是±1,即方程(3+4k2)x2=12的两个根为±1,代入求出k的值.
解答:将直线与椭圆方程联立,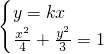 ,
,
化简整理得(3+4k2)x2=12(*)
因为分别过A、B向x轴作垂线,垂足恰为椭圆的两个焦点,
故方程的两个根为±1.代入方程(*),得k=
故选A.
点评:本题考查了直线与圆锥曲线的交点问题,方法是将直线与圆锥曲线方程联立来求解,此方法是数学圆锥曲线中的重要思想方法.
分析:将直线方程与椭圆方程联立,得(3+4k2)x2=12.分别过A、B向x轴作垂线,垂足恰为椭圆的两个焦点,说明A,B的横坐标是±1,即方程(3+4k2)x2=12的两个根为±1,代入求出k的值.
解答:将直线与椭圆方程联立,
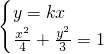 ,
,化简整理得(3+4k2)x2=12(*)
因为分别过A、B向x轴作垂线,垂足恰为椭圆的两个焦点,
故方程的两个根为±1.代入方程(*),得k=

故选A.
点评:本题考查了直线与圆锥曲线的交点问题,方法是将直线与圆锥曲线方程联立来求解,此方法是数学圆锥曲线中的重要思想方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设直线y=kx与椭圆
+
=1相交于A、B两点,分别过A、B向x轴作垂线,若垂足恰为椭圆的两个焦点,则k等于( )
| x2 |
| 4 |
| y2 |
| 3 |
A、±
| ||
B、±
| ||
C、±
| ||
| D、±2 |