题目内容
已知集合A和集合B各含有12个元素,A∩B含4个元素,试求同时满足下面两个条件的集合C的个数:(1)C A B ,且C中含有3个元素;(2)
B ,且C中含有3个元素;(2) (
( 表示空集)。
表示空集)。
 B ,且C中含有3个元素;(2)
B ,且C中含有3个元素;(2) (
( 表示空集)。
表示空集)。1084个
根据集合元素的互异性,A并B中应该有12+12-4=20个元素,又因为满足条件(1)(2)说明C中一定含有A中的元素,并且C中有三个A并B当中的元素,所以按照C中含有元素的个数分类讨论即可。
解:∵A∪B含有12+12-4=20个元素; B含12个元素, ---------------2分
∴ ∩B含20-12=8个元素, ---------------3分
∩B含20-12=8个元素, ---------------3分
若C中恰含A中1个元素,则有C112·C28个, ---------------5分
若C中恰含A中2个元素,则有C212·C18个,--------------7分
若C中恰含A中3个元素,则有C312个,--------------9分
∴符合题设的集合C的个数为C112C28+C212C18+C312=1084个. --------------11分
解:∵A∪B含有12+12-4=20个元素; B含12个元素, ---------------2分
∴
 ∩B含20-12=8个元素, ---------------3分
∩B含20-12=8个元素, ---------------3分若C中恰含A中1个元素,则有C112·C28个, ---------------5分
若C中恰含A中2个元素,则有C212·C18个,--------------7分
若C中恰含A中3个元素,则有C312个,--------------9分
∴符合题设的集合C的个数为C112C28+C212C18+C312=1084个. --------------11分

练习册系列答案
相关题目
 是p的必要条件,求实数a.
是p的必要条件,求实数a.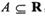 ,对任意
,对任意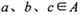 ,运算“
,运算“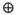 ”具有如下性质:
”具有如下性质: ; (2)
; (2)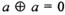 ; (3)
; (3)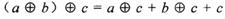 .
.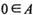 :
: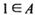 ,则
,则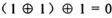 ;
;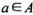 ,且
,且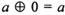 ,则a = 0;
,则a = 0;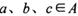 ,且
,且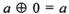 ,
,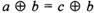 ,则a = c.
,则a = c.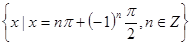 与B=
与B=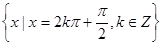 的关系是()
的关系是()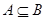
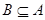
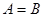
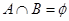
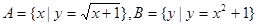 ,则
,则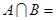 _____________.
_____________. ,
, 则
则 =( )
=( )

 }
}
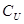 ( M
( M  N )= ( )
N )= ( )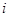 是虚数单位,集合
是虚数单位,集合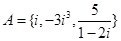 中的元素之和为( )
中的元素之和为( )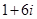
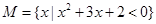 ,集合
,集合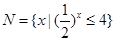 ,则
,则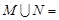 ( )
( )