题目内容
已知在直角坐标平面内,以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,点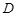 的极坐标是
的极坐标是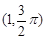 ,曲线C的极坐标方程为
,曲线C的极坐标方程为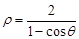 .
.
(I)求点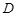 的直角坐标和曲线C的直角坐标方程;
的直角坐标和曲线C的直角坐标方程;
(II)若经过点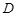 的直线
的直线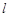 与曲线C交于A、B两点,求
与曲线C交于A、B两点,求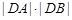 的最小值.
的最小值.
【答案】
(1)  ,
, 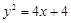
(2) 当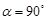 时,
时,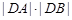 取得最小值3.
取得最小值3.
【解析】
试题分析:解:(I)点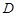 的直角坐标是
的直角坐标是 , (2分)
, (2分)
∵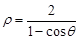 ,∴
,∴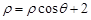 ,即
,即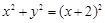 , (5分)
, (5分)
化简得曲线C的直角坐标方程是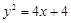 ; (6分)
; (6分)
(II)设直线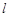 的倾斜角是
的倾斜角是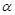 ,则
,则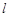 的参数方程变形为
的参数方程变形为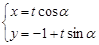 ,(8分)
,(8分)
代入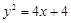 ,得
,得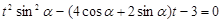
设其两根为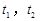 ,则
,则 , (10分)
, (10分)
∴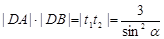 .
.
当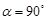 时,
时,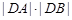 取得最小值3. (13分)
取得最小值3. (13分)
考点:坐标系和参数方程
点评:解决的关键是对于极坐标和直角坐标的转化,以及利用参数方程求解最值,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
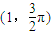 ,曲线C的极坐标方程为
,曲线C的极坐标方程为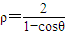 .
.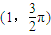 ,曲线C的极坐标方程为
,曲线C的极坐标方程为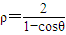 .
.