题目内容
已知f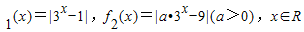 ,且f(x)=
,且f(x)=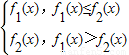
(1)当a=1时,求f(x)的解析式;
(2)在(1)的条件下,若方程f(x)-m=0有4个不等的实根,求实数m的范围;
(3)当2≤a<9时,设f(x)=f2(x)所对应的自变量取值区间的长度为l(闭区间[m,n]的长度定义为n-m),试求l的最大值.
【答案】分析:(1)当a=1时,根据函数f1(x)和函数f2(x)的解析式以及条件f(x)=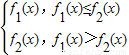 可得f(x)的解析式.
可得f(x)的解析式.
(2)在(1)的条件下,由题意可得,函数y=f(x)与直线y=m有4个不同的交点,数形结合可得实数m的范围.
(3)由于2≤a<9,分 x≥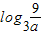 时、当0≤x≤
时、当0≤x≤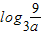 时、当x<0时,分别由 f2(x)-f1(x)≤0 求得x的范围,再把所得的x的范围取并集,从而得到区间长度l的解析式,
时、当x<0时,分别由 f2(x)-f1(x)≤0 求得x的范围,再把所得的x的范围取并集,从而得到区间长度l的解析式,
再根据函数的单调性求得l的最大值.
解答:解:(1)当a=1时,f1(x)=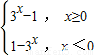 ,f2(x)=
,f2(x)= ,∴当x=log35时,f1(x)=f2(x).
,∴当x=log35时,f1(x)=f2(x).
∴f(x)=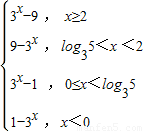 .
.
(2)在(1)的条件下,若方程f(x)-m=0有4个不等的实根,则函数y=f(x)与直线y=m有4个不同的交点.
数形结合可得,0<m<1,故实数m的范围是(0,1).
(3)由于2≤a<9,当 x≥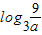 时,∵a•3x-9≥0,3x-1>0,
时,∵a•3x-9≥0,3x-1>0,
∴由 f2(x)-f1(x)=(a•3x-9)-( 3x-1)≤0 可得 x≤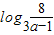 ,
,
从而当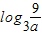 ≤x≤
≤x≤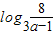 时,f(x)=f2(x).
时,f(x)=f2(x).
当0≤x≤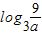 时,∵a•3x-9<0,3x-1≥0,
时,∵a•3x-9<0,3x-1≥0,
∴由 f2(x)-f1(x)=-(a•3x-9)-( 3x-1)=10-(a+1)3x≤0 解得 x≥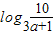 ,
,
从而当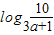 ≤x≤
≤x≤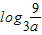 时,f(x)=f2(x).
时,f(x)=f2(x).
当x<0时,由 f2(x)-f1(x)=-(a•3x-9)-(1-3x)=8-(a-1)3x>0,故f(x)=f2(x) 一定不成立.
综上可得,当且仅当 x∈[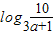 ,
,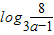 ]时,有f(x)=f2(x) 一定成立.
]时,有f(x)=f2(x) 一定成立.
故 l=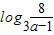 -
-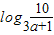 =
=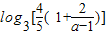 ,
,
从而当a=2时,l取得最大值为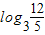 .
.
点评:本题主要考查对数函数、指数函数的图象和性质综合应用,体现了分类讨论的数学思想,属于中档题.
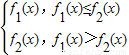 可得f(x)的解析式.
可得f(x)的解析式.(2)在(1)的条件下,由题意可得,函数y=f(x)与直线y=m有4个不同的交点,数形结合可得实数m的范围.
(3)由于2≤a<9,分 x≥
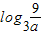 时、当0≤x≤
时、当0≤x≤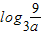 时、当x<0时,分别由 f2(x)-f1(x)≤0 求得x的范围,再把所得的x的范围取并集,从而得到区间长度l的解析式,
时、当x<0时,分别由 f2(x)-f1(x)≤0 求得x的范围,再把所得的x的范围取并集,从而得到区间长度l的解析式,再根据函数的单调性求得l的最大值.
解答:解:(1)当a=1时,f1(x)=
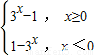 ,f2(x)=
,f2(x)= ,∴当x=log35时,f1(x)=f2(x).
,∴当x=log35时,f1(x)=f2(x).∴f(x)=
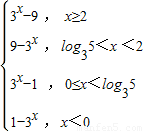 .
.(2)在(1)的条件下,若方程f(x)-m=0有4个不等的实根,则函数y=f(x)与直线y=m有4个不同的交点.
数形结合可得,0<m<1,故实数m的范围是(0,1).
(3)由于2≤a<9,当 x≥
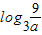 时,∵a•3x-9≥0,3x-1>0,
时,∵a•3x-9≥0,3x-1>0,∴由 f2(x)-f1(x)=(a•3x-9)-( 3x-1)≤0 可得 x≤
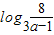 ,
,从而当
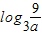 ≤x≤
≤x≤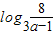 时,f(x)=f2(x).
时,f(x)=f2(x).当0≤x≤
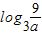 时,∵a•3x-9<0,3x-1≥0,
时,∵a•3x-9<0,3x-1≥0,∴由 f2(x)-f1(x)=-(a•3x-9)-( 3x-1)=10-(a+1)3x≤0 解得 x≥
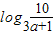 ,
,从而当
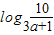 ≤x≤
≤x≤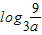 时,f(x)=f2(x).
时,f(x)=f2(x).当x<0时,由 f2(x)-f1(x)=-(a•3x-9)-(1-3x)=8-(a-1)3x>0,故f(x)=f2(x) 一定不成立.
综上可得,当且仅当 x∈[
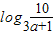 ,
,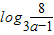 ]时,有f(x)=f2(x) 一定成立.
]时,有f(x)=f2(x) 一定成立.故 l=
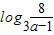 -
-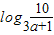 =
=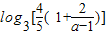 ,
,从而当a=2时,l取得最大值为
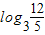 .
.点评:本题主要考查对数函数、指数函数的图象和性质综合应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目