题目内容
(本小题满分16分)
(1)用二项式定理证明: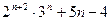
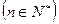 能被25整除
能被25整除
(2)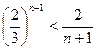 (
(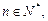 且
且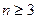
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在区间[-3,3]上任取两数x,y,使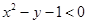 成立的概率为
成立的概率为
A.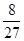 | B.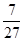 | C. | D.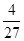 |
题目内容
(本小题满分16分)
(1)用二项式定理证明: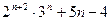
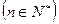 能被25整除
能被25整除
(2)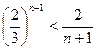 (
(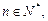 且
且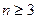
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案在区间[-3,3]上任取两数x,y,使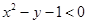 成立的概率为
成立的概率为
A.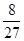 | B.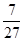 | C. | D.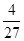 |