题目内容
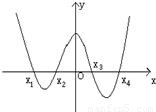
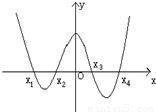
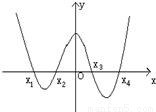
函数g（x）中x∈R，其导函数g′（x）的图象如图，则函数g（x）（ ）
| A．无极大值，有四个极小值点 |
| B．有两个极大值，两个极小值点 |
| C．有三个极大值，两个极小值点 |
| D．有四个极大值点，无极小值点 |
根据图象可知：当x＜x1时，g′（x）＞0，函数递增，当x＞x1时，g′（x）＜0，函数递减，所以函数在x=x1取极大值；同理可得x=x3时，函数取极大值；
当x＜x2时，g′（x）＜0，函数递减，x＞x2时，g′（x）＞0，函数递增，所以x=x2时，函数有极小值；同理可得x=x4时，函数取极小值．
所以函数有两个极大值，两个极小值．
故选B
当x＜x2时，g′（x）＜0，函数递减，x＞x2时，g′（x）＞0，函数递增，所以x=x2时，函数有极小值；同理可得x=x4时，函数取极小值．
所以函数有两个极大值，两个极小值．
故选B
练习册系列答案
名校课堂系列答案
相关题目
9、函数g（x）中x∈R，其导函数g′（x）的图象如图，则函数g（x）（ ）
