题目内容
已知在 的展开式中只有第6项的二项式系数最大,则这个展开式中x8的系数是 .
的展开式中只有第6项的二项式系数最大,则这个展开式中x8的系数是 .
【答案】分析:根据二项式系数的性质:中间项的二项式系数最大求出n的值,再利用二项展开式的通项公式求出通项,令通项中x的系数为8求出r的值,代入通项求出展开式中x8的系数.
解答:解:因为在 的展开式中只有第6项的二项式系数最大,
的展开式中只有第6项的二项式系数最大,
所以展开式共有11项,
所以n=10,
所以 =
= ,
,
其展开式的通项为 =(-1)r210-rC10rx2r-10,
=(-1)r210-rC10rx2r-10,
令2r-10=8解得r=9
所以展开式中x8的系数是-2C109=-20,
故答案为-20
点评:本题考查二项式系数的性质、二项展开式的通项公式并用通项公式解决二项展开式的特定项问题.
解答:解:因为在
 的展开式中只有第6项的二项式系数最大,
的展开式中只有第6项的二项式系数最大,所以展开式共有11项,
所以n=10,
所以
 =
= ,
,其展开式的通项为
 =(-1)r210-rC10rx2r-10,
=(-1)r210-rC10rx2r-10,令2r-10=8解得r=9
所以展开式中x8的系数是-2C109=-20,
故答案为-20
点评:本题考查二项式系数的性质、二项展开式的通项公式并用通项公式解决二项展开式的特定项问题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
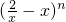 的展开式中只有第6项的二项式系数最大,则这个展开式中x8的系数是________.
的展开式中只有第6项的二项式系数最大,则这个展开式中x8的系数是________.