题目内容
设0≤θ＜2π，已知两个向量| OP1 |
| OP2 |
| P1P2 |
分析：根据两个向量的坐标写出两个向量的差的坐标形式，表示出向量的模长，表示式中含有三角函数，整理变化根据角的范围得到模长的最大值．
解答：解：∵两个向量
=(cosθ ， sinθ)，
=(2+sinθ ， 2-cosθ)，
∴向量
=（2+sinθ-cosθ，2-consθ-sinθ），
∴|
|=
=
=
，
∵0≤θ＜2π，
∴cosθ=-1时，模长的最大值是
=3
，
故答案为：3
| OP1 |
| OP2 |
∴向量
| P1P2 |
∴|
| P1P2 |
| (2+sinθ-cosθ)2+(2-cosθ-sinθ)2 |
=
| 8-8cosθ+2 |
=
| 10-8cosθ |
∵0≤θ＜2π，
∴cosθ=-1时，模长的最大值是
| 18 |
| 2 |
故答案为：3
| 2 |
点评：本题是一个三角函数同向量结合的问题，是以求向量的模长为条件，得到三角函数的关系式，是一道综合题，在高考时可以以选择和填空形式出现．
练习册系列答案
阅读快车系列答案
相关题目
设0＜θ＜
，已知a1=2cosθ，an+1=
（n∈N*），猜想an等于（ ）
| π |
| 2 |
| 2+an |
A、2cos
| ||
B、2cos
| ||
C、2cos
| ||
D、2sin
|
，n∈N*，其中常数α，β均为非零实数，且α＋β≠0.
， a1＝1，a2＝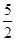
，求证：数列{| an＋1－an－1|}
(n∈N*，n≥2)与数列{n＋
} (n∈N*)中没有相同数值的项.