题目内容
19.设y=arctan$\frac{x+1}{x-1}$,则$\frac{dy}{dx}$=-$\frac{1}{1+{x}^{2}}$.分析 利用换元法,结合复合函数的导数公式,即可得出结论.
解答 解:令u=$\frac{x+1}{x-1}$,则y=arctanu
∴u=tany
∴$\frac{du}{dy}$=sec2y=tan2y+1
∴$\frac{dy}{du}$=$\frac{1}{1+{u}^{2}}$,
∴$\frac{dy}{dx}$=$\frac{1}{1+{u}^{2}}$•$\frac{x-1-x-1}{(x-1)^{2}}$=-$\frac{1}{1+{x}^{2}}$.
故答案为:-$\frac{1}{1+{x}^{2}}$.
点评 本题考查复合函数的导数公式,考查学生的计算能力,属于中档题.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
9.命题“x2+y2=0,则x=y=0”的否定命题为( )
| A. | 若x2+y2=0,则x≠0且y≠0 | B. | 若x2+y2=0,则x≠0或y≠0 | ||
| C. | 若x2+y2≠0,则x≠0且y≠0 | D. | 若x2+y2≠0,则x≠0或y≠0 |
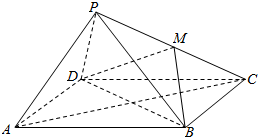 如图已知四边形ABCD是菱形,P是ABCD所在平面外一点,且PB=PD=AB,M是PC的中点,
如图已知四边形ABCD是菱形,P是ABCD所在平面外一点,且PB=PD=AB,M是PC的中点,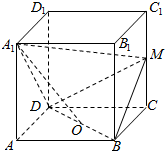 如图,在正方体ABCD-A1B1C1D1中,M为CC1的中点.
如图,在正方体ABCD-A1B1C1D1中,M为CC1的中点.