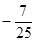题目内容
.(本小题满分12分)
已知函数 .
.
(Ⅰ)求函数 的最大值,并写出
的最大值,并写出 取最大值时
取最大值时 的取值集合;
的取值集合;
(Ⅱ)已知 中,角
中,角 的对边分别为
的对边分别为 若
若
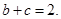 求实数
求实数 的最小值.
的最小值.
已知函数
 .
.(Ⅰ)求函数
 的最大值,并写出
的最大值,并写出 取最大值时
取最大值时 的取值集合;
的取值集合;(Ⅱ)已知
 中,角
中,角 的对边分别为
的对边分别为 若
若
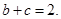 求实数
求实数 的最小值.
的最小值.(Ⅰ) . (Ⅱ)当
. (Ⅱ)当 时,实数
时,实数 取最小值1。
取最小值1。
 . (Ⅱ)当
. (Ⅱ)当 时,实数
时,实数 取最小值1。
取最小值1。(1)利用三角函数公式把 化为
化为 的形式,由正弦函数的性质求出其最值和对应的
的形式,由正弦函数的性质求出其最值和对应的 的值;(2)由(1)结合三角形中角的范围求出
的值;(2)由(1)结合三角形中角的范围求出 ,再由余弦定理表示出
,再由余弦定理表示出 ,利用不等式求出其最值.
,利用不等式求出其最值.
(Ⅰ)
 .
.
∴函数 的最大值为
的最大值为 .
.
要使 取最大值,则
取最大值,则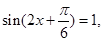
 ,解得
,解得 .
.
故 的取值集合为
的取值集合为 . ……………………………………………(6分)
. ……………………………………………(6分)
(Ⅱ)由题意, ,化简得
,化简得
 ,
, , ∴
, ∴ , ∴
, ∴
在 中,根据余弦定理,得
中,根据余弦定理,得 .
.
由 ,知
,知 ,即
,即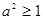 .
.
∴当 时,实数
时,实数 取最小值
取最小值 ………………………………………………(12分)
………………………………………………(12分)
 化为
化为 的形式,由正弦函数的性质求出其最值和对应的
的形式,由正弦函数的性质求出其最值和对应的 的值;(2)由(1)结合三角形中角的范围求出
的值;(2)由(1)结合三角形中角的范围求出 ,再由余弦定理表示出
,再由余弦定理表示出 ,利用不等式求出其最值.
,利用不等式求出其最值.(Ⅰ)

 .
.∴函数
 的最大值为
的最大值为 .
.要使
 取最大值,则
取最大值,则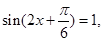
 ,解得
,解得 .
.故
 的取值集合为
的取值集合为 . ……………………………………………(6分)
. ……………………………………………(6分)(Ⅱ)由题意,
 ,化简得
,化简得
 ,
, , ∴
, ∴ , ∴
, ∴
在
 中,根据余弦定理,得
中,根据余弦定理,得 .
.由
 ,知
,知 ,即
,即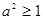 .
.∴当
 时,实数
时,实数 取最小值
取最小值 ………………………………………………(12分)
………………………………………………(12分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图象向左平移
的图象向左平移 个单位,所得图象的函数解析式为 ( )
个单位,所得图象的函数解析式为 ( )
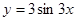


 在一个周期内的图象如图,求函数的解析式
在一个周期内的图象如图,求函数的解析式
 在
在 上的递增区间为 .
上的递增区间为 . 的最大值为3,
的最大值为3, 的图像与
的图像与 轴的交点坐标为
轴的交点坐标为 ,其相邻两条对称轴间的距离为
,其相邻两条对称轴间的距离为 ,则
,则
 ____________.
____________.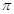 且在
且在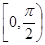 单调递增的是
单调递增的是



 中,如果满足
中,如果满足 ,则
,则 的取值范围是 .
的取值范围是 . ,且
,且 ,则
,则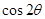 的值为( )
的值为( )