题目内容
函数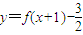
为奇函数，y=f-1（x）是y=f（x）的反函数，若f（3）=0，则f-1（3）=（ ）A．-1
B．1
C．-2
D．2
【答案】分析：观察结论，求f-1（3）的值，即解方程f（x）=3，问题转化为寻求函数值为3的自变量的值，由题设条件知f（2）=f（3）-
=-
，依次研究知f（1）=f（2）-
=-3，，由此可以解出f（-1）=-3，下由奇函数的性质与反函数的定义可求答案．
解答：解：∵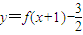
，
∴f（2）=f（3）-
=-
，
∴f（1）=f（2）-
=-3，
又函数
为奇函数，
故f（-1）=3，
∴f-1（3）=-1，
故应选A．
点评：考查函数的性质与反函数的定义，本题的解题技巧是把求函数值的问题通过反函数的定义将其转化为知函数值求自变量的问题，降低了运算难度．
=-，依次研究知f（1）=f（2）-=-3，，由此可以解出f（-1）=-3，下由奇函数的性质与反函数的定义可求答案．解答：解：∵
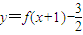，∴f（2）=f（3）-
=-，∴f（1）=f（2）-
=-3，又函数
为奇函数，故f（-1）=3，
∴f-1（3）=-1，
故应选A．
点评：考查函数的性质与反函数的定义，本题的解题技巧是把求函数值的问题通过反函数的定义将其转化为知函数值求自变量的问题，降低了运算难度．
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
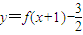为奇函数，y=f-1（x）是y=f（x）的反函数，若f（3）=0，则f-1（3）=（ ）
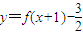为奇函数，y=f-1（x）是y=f（x）的反函数，若f（3）=0，则f-1（3）=（ ）