题目内容
圆锥曲线 的焦点坐标是 .
的焦点坐标是 .
【答案】分析:由三角函数的公式可化参数方程为普通方程,再由标准情况下的焦点坐标得出所求曲线的焦点坐标.
解答:解:由 可得
可得 ,
,
由三角函数的运算可得tan2θ+1=sec2θ,
代入可得 ,即
,即 ,
,
可看作双曲线 向右平移1个单位得到,
向右平移1个单位得到,
而双曲线 的焦点为(-5,0),(5,0)
的焦点为(-5,0),(5,0)
故所求双曲线的焦点为(-4,0),(6,0)
故答案为:(-4,0),(6,0)
点评:本题考查双曲线的参数方程,以及双曲线的非标准方程,属中档题.
解答:解:由
 可得
可得 ,
,由三角函数的运算可得tan2θ+1=sec2θ,
代入可得
 ,即
,即 ,
,可看作双曲线
 向右平移1个单位得到,
向右平移1个单位得到,而双曲线
 的焦点为(-5,0),(5,0)
的焦点为(-5,0),(5,0)故所求双曲线的焦点为(-4,0),(6,0)
故答案为:(-4,0),(6,0)
点评:本题考查双曲线的参数方程,以及双曲线的非标准方程,属中档题.

练习册系列答案
相关题目
 的焦点坐标是 .
的焦点坐标是 . 的焦点坐标是( )
的焦点坐标是( )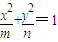 的焦点坐标是( )
的焦点坐标是( ) 的焦点坐标是( )
的焦点坐标是( )