题目内容
(2012•成都模拟)已知底面边长为2,侧棱长为
的正四棱锥P-ABCD内接于球O,则球面上A、B两点间的球面距离是( )
| 6 |
分析:设球的半径为R,利用正四棱锥的性质和球的性质,结合勾股定理列方程,解之得球半径,进而求出球心角,利用球面距离公式,可得结论.
解答: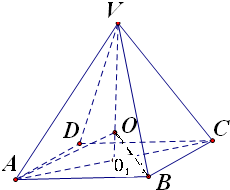 解:设外接球球心为O,正方形ABCD中心为O1,连接VO1,则球心O在VO1上,连接AC、OA、OB
解:设外接球球心为O,正方形ABCD中心为O1,连接VO1,则球心O在VO1上,连接AC、OA、OB
∵正方形ABCD边长为2,∴对角线AC=2
,O1A=
AC=
∵VO1⊥平面ABCD,
∴Rt△VO1A中,VO1=
=2
设外接球半径为R,则Rt△OO1A中,OA=R,O1O=2-R
∴R2=(2-R)2+2,解之得:R=
因此,△AOB中,cos∠AOB=
=
故∠AOB=arccos
所以AB两点的球面距离为R×∠AOB=
arccos
故选B.
 解:设外接球球心为O,正方形ABCD中心为O1,连接VO1,则球心O在VO1上,连接AC、OA、OB
解:设外接球球心为O,正方形ABCD中心为O1,连接VO1,则球心O在VO1上,连接AC、OA、OB∵正方形ABCD边长为2,∴对角线AC=2
| 2 |
| 1 |
| 2 |
| 2 |
∵VO1⊥平面ABCD,
∴Rt△VO1A中,VO1=
| 6-2 |
设外接球半径为R,则Rt△OO1A中,OA=R,O1O=2-R
∴R2=(2-R)2+2,解之得:R=
| 3 |
| 2 |
因此,△AOB中,cos∠AOB=
| ||||
2×
|
| 1 |
| 9 |
故∠AOB=arccos
| 1 |
| 9 |
所以AB两点的球面距离为R×∠AOB=
| 3 |
| 2 |
| 1 |
| 9 |
故选B.
点评:本题考查球面距离,考查了正四棱锥的性质和球的性质,余弦定理和反三角函数的应用等知识点,属于中档题.

练习册系列答案
相关题目