Question

17．已知点A（2，0）抛物线C：x²=4y的焦点为F，射线FA与抛物线C相交于点M，与其准线相交于点N，则|FM|：|MN|=1：$\sqrt{5}$．

Answer 1

分析 求出抛物线C的焦点F的坐标，从而得到AF的斜率k=-$\frac{1}{2}$．过M作MP⊥l于P，根据抛物线物定义得|FM|=|PM|．Rt△MPN中，根据tan∠MNP=$\frac{1}{2}$，从而得到|PN|=2|PM|，进而算出|MN|=$\sqrt{5}$|PM|，由此即可得到|FM|：|MN|的值．

解答 解：∵抛物线C：x²=4y的焦点为F（0，1），点A坐标为（2，0），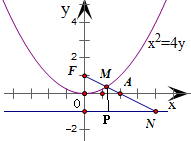
∴抛物线的准线方程为l：y=-1，直线AF的斜率为k=$\frac{0-1}{2-0}$=-$\frac{1}{2}$，
过M作MP⊥l于P，根据抛物线物定义得|FM|=|PM|，
∵Rt△MPN中，tan∠MNP=-k=$\frac{1}{2}$，
∴$\frac{|PM|}{|PN|}$=$\frac{1}{2}$，可得|PN|=2|PM|，
得|MN|=$\sqrt{{|PN|}^{2}{+|PM|}^{2}}$=$\sqrt{5}$|PM|
因此可得|FM|：|MN|=|PM|：|MN|=1：$\sqrt{5}$．
故答案为：1：$\sqrt{5}$．

点评 本题给出抛物线方程和射线FA，求线段的比值．着重考查了直线的斜率、抛物线的定义、标准方程和简单几何性质等知识，属于中档题．