题目内容
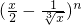 的展开式中,只有第五项的二项式系数最大,则展开式中的常数项是________.
的展开式中,只有第五项的二项式系数最大,则展开式中的常数项是________.
7
分析:根据题意,( )n的展开式中只有第5项的二项式系数最大,则n=8,可得(
)n的展开式中只有第5项的二项式系数最大,则n=8,可得( )8的二项展开式,令
)8的二项展开式,令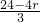 =0,解可得,r=6;将其代入二项展开式,可得答案.
=0,解可得,r=6;将其代入二项展开式,可得答案.
解答:根据题意,( )n的展开式中只有第5项的二项式系数最大,
)n的展开式中只有第5项的二项式系数最大,
则n=8,
则( )8的二项展开式为Tr+1=C88-r•(
)8的二项展开式为Tr+1=C88-r•( )8-r•(-
)8-r•(- )r=(-1)r•(
)r=(-1)r•( )8-r•C88-r•
)8-r•C88-r•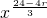 ,
,
令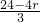 =0,解可得,r=6;
=0,解可得,r=6;
则其常数项为7.
故答案为:7.
点评:本题考查二项式定理的应用,涉及二项式系数的性质,要注意系数与二项式系数的区别.
分析:根据题意,(
 )n的展开式中只有第5项的二项式系数最大,则n=8,可得(
)n的展开式中只有第5项的二项式系数最大,则n=8,可得( )8的二项展开式,令
)8的二项展开式,令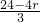 =0,解可得,r=6;将其代入二项展开式,可得答案.
=0,解可得,r=6;将其代入二项展开式,可得答案.解答:根据题意,(
 )n的展开式中只有第5项的二项式系数最大,
)n的展开式中只有第5项的二项式系数最大,则n=8,
则(
 )8的二项展开式为Tr+1=C88-r•(
)8的二项展开式为Tr+1=C88-r•( )8-r•(-
)8-r•(- )r=(-1)r•(
)r=(-1)r•( )8-r•C88-r•
)8-r•C88-r•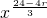 ,
,令
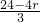 =0,解可得,r=6;
=0,解可得,r=6;则其常数项为7.
故答案为:7.
点评:本题考查二项式定理的应用,涉及二项式系数的性质,要注意系数与二项式系数的区别.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
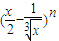 的展开式中,只有第五项的二项式系数最大,则展开式中的常数项是______.
的展开式中,只有第五项的二项式系数最大,则展开式中的常数项是______.