题目内容
(1设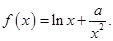
(1)当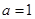 时,求f(x)的单调区间;
时,求f(x)的单调区间;
(2)求f(x)的零点个数
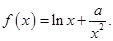
(1)当
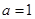 时,求f(x)的单调区间;
时,求f(x)的单调区间;(2)求f(x)的零点个数
(1)减区间 ,增区间
,增区间 ;(2)见解析
;(2)见解析
 ,增区间
,增区间 ;(2)见解析
;(2)见解析 试题分析:(1)先求出函数
 的定义域,然后在
的定义域,然后在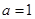 的条件下对函数
的条件下对函数 求导,求出使得导数为0的自变量的取值,再根据函数的单调性与导数的关系判断函数
求导,求出使得导数为0的自变量的取值,再根据函数的单调性与导数的关系判断函数 的单调区间;(2) 对
的单调区间;(2) 对 的取值进行分类讨论,当
的取值进行分类讨论,当 时分
时分 和
和 两种情况,由
两种情况,由 ,
,  ,结合零点存在性定理可知
,结合零点存在性定理可知 在
在 上有一个零点;当
上有一个零点;当 时,根据函数的单调性求得函数的极小值
时,根据函数的单调性求得函数的极小值 ,对极小值与0的关系分三种情况进行分类讨论,结合零点存在性定理求得每种情况下的函数的零点个数
,对极小值与0的关系分三种情况进行分类讨论,结合零点存在性定理求得每种情况下的函数的零点个数 试题解析:(1)
 的定义域是
的定义域是 , 1分
, 1分当
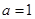 时,∵
时,∵ 2分
2分令
 ,(负舍去) 3分
,(负舍去) 3分当
 时,
时,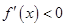 ;当
;当 时,
时, 4分
4分所以
 是
是 的减区间,
的减区间, 是
是 的增区间, 5分
的增区间, 5分所以
 的减区间是
的减区间是 ,
, 的增区间是
的增区间是 6分
6分(2)
 的定义域是
的定义域是 ,∵
,∵ 7分
7分当
 时,
时, 在
在 上是增函数,当
上是增函数,当 时有零点
时有零点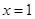 , 8分
, 8分当
 时,
时, 9分
9分(或当
 时,
时, ;当
;当 时,
时, ),
),所以
 在
在 上有一个零点, 10分
上有一个零点, 10分当
 时,由(1)知,
时,由(1)知, 在
在 上是减函数,
上是减函数, 在
在 上是增函数,所以当
上是增函数,所以当 时,
时, 有极小值,即最小值
有极小值,即最小值 11分
11分当
 ,即
,即 时,
时, 无零点,
无零点,当
 ,即
,即 时,
时, 有一个零点,
有一个零点,当
 ,即
,即 时,
时, 有2个零点 13分
有2个零点 13分综上可知,当
 时,
时, 无零点;当
无零点;当 时,
时, 有一个零点;当
有一个零点;当 时,
时, 有2个零点 14分
有2个零点 14分
练习册系列答案
相关题目
 ,
, .
. ;
; 与
与 、
、 均相切,切点分别为(
均相切,切点分别为( )、(
)、( ),且
),且 ,求证:
,求证: .
.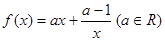 ,
,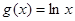 .
.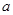 ,函数
,函数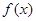 与
与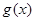 的图象在
的图象在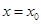 处的切线斜率总相等,求
处的切线斜率总相等,求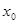 的值;
的值;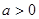 ,对任意
,对任意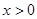 ,不等式
,不等式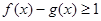 恒成立,求实数
恒成立,求实数 的一个焦点是
的一个焦点是 ,一条渐近线的方程是
,一条渐近线的方程是 .
. 为斜率的直线
为斜率的直线 与双曲线
与双曲线 ,且线段
,且线段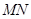 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为 ,求
,求 的取值范围.
的取值范围. ,
, 的单调性;
的单调性; .
.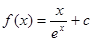
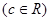
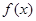 的单调区间、最大值;
的单调区间、最大值;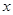 的方程
的方程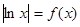 的根的个数.
的根的个数. ,若
,若 在
在 上的极值点分别为
上的极值点分别为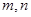 ,则
,则 的值为( )
的值为( )
 ,给出定义:
,给出定义: 是函数
是函数 的导函数,
的导函数, 是
是 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”。某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心。若
的“拐点”。某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心。若 ,请你根据这一发现,求:(1)函数
,请你根据这一发现,求:(1)函数 =________.
=________. 所表示的平面区域为D,直线
所表示的平面区域为D,直线 与D有公共点,则
与D有公共点,则 的取值范围是________
的取值范围是________