题目内容
过点P（2，-2）和曲线y=3x-x3相切的直线方程为 ．
【答案】分析：先考虑点（2，-2）是切点的情形，求出切线方程，然后设切点为（x，y），根据切点与点（2，-2）的斜率等于切线的斜率建立等量关系，解之即可求出切点，从而求出切线方程．
解答：解：设直线l：y+2=k（x-2）．∵y′=3-3x2，∴y′|x=2=-9，
又∵直线与曲线均过点（2，-2），于是直线y+2=k（x-2）与曲线y=3x-x3相切于切点（2，-2）时，k=-9．
若直线与曲线切于点（x，y）（x≠2），则k=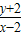
，∵y=3x-x3，
∴
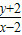=-x2-2x-1，
又∵k=y′|x=x=3-3x2，
∴-x2-2x-1=3-3x2，∴2x2-2x-4=0，
∵x≠2，∴x=-1，∴k=3-3x2=0，
故直线l的方程为9x+y-16=0或y=-2．
故答案为：9x+y-16=0或y=-2．
点评：本题主要考查了利用导数研究曲线上某点切线方程，解题的关键注意过某点和在某点的区别，属于中档题．
解答：解：设直线l：y+2=k（x-2）．∵y′=3-3x2，∴y′|x=2=-9，
又∵直线与曲线均过点（2，-2），于是直线y+2=k（x-2）与曲线y=3x-x3相切于切点（2，-2）时，k=-9．
若直线与曲线切于点（x，y）（x≠2），则k=
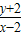，∵y=3x-x3，∴
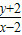=-x2-2x-1，又∵k=y′|x=x=3-3x2，
∴-x2-2x-1=3-3x2，∴2x2-2x-4=0，
∵x≠2，∴x=-1，∴k=3-3x2=0，
故直线l的方程为9x+y-16=0或y=-2．
故答案为：9x+y-16=0或y=-2．
点评：本题主要考查了利用导数研究曲线上某点切线方程，解题的关键注意过某点和在某点的区别，属于中档题．
练习册系列答案
相关题目