题目内容
若函数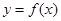 在区间
在区间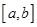 上的图象为连续不断的曲线,则下列说法正确的是( )
上的图象为连续不断的曲线,则下列说法正确的是( )
A 若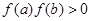 ,不存在实数
,不存在实数 使得
使得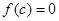 ;
;
B 若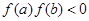 ,存在且只存在一个实数
,存在且只存在一个实数 使得
使得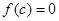 ;
;
C 若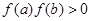 ,有可能存在实数
,有可能存在实数 使得
使得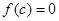 ;
;
D 若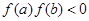 ,有可能不存在实数
,有可能不存在实数 使得
使得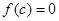 ;
;
C
解析解:由零点存在性定理可知选项D不正确;
对于选项B,可通过反例“f(x)=x(x-1)(x+1)在区间[-2,2]上满足f(-2)f(2)<0,但其存在三个解{-1,0,1}”推翻;
同时选项A可通过反例“f(x)=(x-1)(x+1)在区间[-2,2]上满足f(-2)f(2)>0,但其存在两个解{-1,1}”;
故选C.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
下列三个图象中,能表示y是x的函数图象的个数是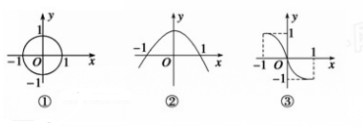


| A.0 | B.1 | C.2 | D.3 |
若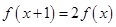 ,则
,则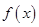 等于 ( )
等于 ( )
A. | B.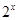 | C.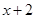 | D.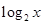 |
下列各函数中,值域为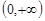 的是
的是
A.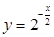 | B.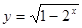 | C.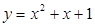 | D.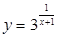 |
下列四组函数中表示同一函数的是( )
A. , ,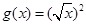 | B.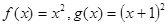 |
C.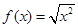 , ,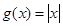 | D.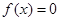 , ,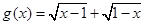  |
设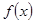 是定义在区间
是定义在区间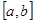 上的函数,且
上的函数,且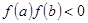 ,则方程
,则方程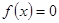 在区间
在区间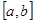 上( )
上( )
| A.至少有一实根 | B.至多有一实根 |
| C.没有实根 | D.必有唯一实根 |
函数 的定义域为( )
的定义域为( )
A.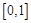 | B.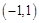 | C. | D.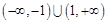 |
 表示的曲线为图中的( )
表示的曲线为图中的( )
 函数
函数 ,若x=-1为函数
,若x=-1为函数 的一个极值点,则下列图象不可能为:
的一个极值点,则下列图象不可能为: 的图象的是
的图象的是