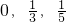题目内容
设集合M={x|
∈Z,x∈Z},则集合M 中元素个数为
| 8 | x+3 |
8
8
个.分析:依据题意知,
只能为±1、±2、±4、±8,分别求出x即可.
| 8 |
| x+3 |
解答:解:由于
∈Z,x∈Z,则
只能为±1、±2、±4、±8
当
=1时,x=5;当
=-1时,x=-11;
当
=2时,x=1;当
=-2时,x=-7;
当
=4时,x=-1;当
=-4时,x=-5;
当
=8时,x=-2;当
=-8时,x=-4;均满足题意.
故答案为 8
| 8 |
| x+3 |
| 8 |
| x+3 |
当
| 8 |
| x+3 |
| 8 |
| x+3 |
当
| 8 |
| x+3 |
| 8 |
| x+3 |
当
| 8 |
| x+3 |
| 8 |
| x+3 |
当
| 8 |
| x+3 |
| 8 |
| x+3 |
故答案为 8
点评:本题考查组合数公式的应用、元素与集合关系的判断等基础知识,考查运算求解能力,属于基础题.

练习册系列答案
相关题目
设集合M={x|x2-8x+15=0},N={x|ax-1=0},若M∩N=N,则实数a的组成的集合Q是( )
| A、{3,5} | ||||
| B、{0,3,5} | ||||
C、{
| ||||
D、{0,
|