题目内容
在等比数列 中,若
中,若 是互不相等的正整数,则有等式
是互不相等的正整数,则有等式 成立.类比上述性质,相应地,在等差数列
成立.类比上述性质,相应地,在等差数列 中,若
中,若 是互不相等的正整数,则有等式________成立.
是互不相等的正整数,则有等式________成立.
(r-s)bt+(s-t)br+(t-r)bs=0
解析试题分析:一般的,等比数列中的积类比等差数列中的和,等比数列中的商类比等差数列的差,等比数列中的幂,类比等差数列中的“积”,所以在等差数列 中,若
中,若 是互不相等的正整数,则有等式(r-s)bt+(s-t)br+(t-r)bs=0成立。
是互不相等的正整数,则有等式(r-s)bt+(s-t)br+(t-r)bs=0成立。
考点:本题主要考查等比数列类比到等差数列的类比推理。
点评:中档题,解答此类问题的一般步骤:①找出等差数列、等比数列之间的相似性或者一致性.②用等比数列的性质去推测等差数列的性质,得出一个明确的命题(或猜想)

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
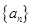 中,
中,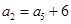 ,则其公差为 .
,则其公差为 . 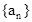 中,已知前15项的和
中,已知前15项的和 ,则
,则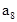 等于_____________
等于_____________ 的前n项和为
的前n项和为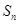 ,且
,且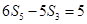 ,则
,则 =________.
=________.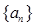 为等差数列,若
为等差数列,若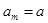 ,
,
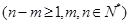 ,则
,则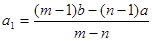 .类比上述结论,对于等比数列
.类比上述结论,对于等比数列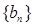
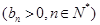 ,若
,若
 ,则可以得到
,则可以得到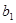 =____________.
=____________. 的前
的前 项和为
项和为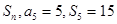 ,则数列
,则数列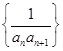 的前100项和为 .
的前100项和为 . 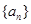 中,有
中,有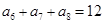 ,则此数列的前13项之和为 .
,则此数列的前13项之和为 . 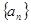 中,a1>0,d≠0,S3=S11,则Sn中的最大值是 。
中,a1>0,d≠0,S3=S11,则Sn中的最大值是 。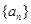 满足
满足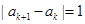 (
(
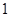 ,2,…,
,2,…,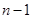 ),若
),若 ,
, ,则
,则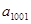 =
=