Question

已知向量a＝(－3,2)，b＝(2,1)，c＝(3，－1)，t∈R.

(1)求|a＋tb|的最小值及相应的t值；

(2)若a－tb与c共线，求实数t.

 

Answer 1

【答案】

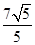（1）当t＝时，|a＋tb|取得最小值.（2）.

【解析】(1)a＋tb＝(2t－3,2＋t)，|a＋tb|²＝(2t－3)²＋(2＋t)²＝5t²－8t＋13＝5²＋，当t＝时，|a＋tb|取得最小值.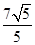

(2)a－tb＝(－3－2t,2－t)，因为a－tb与c共线，所以3＋2t－6＋3t＝0，即t＝.