题目内容
根据向量数乘的定义，可以证明向量数乘有如下运算律：（1）
分析：证明等式成立，把两边看成两个向量，先证模相等，再证明方向也相同．
解答：解：（1）λ（μ
）=（λμ）
，（2）（λ+μ）
=λ
+μ
，（3）λ （
+
）=λ
+μ
．
证明：（1）若λ=0 或μ=0，或
=
，等式显然成立．若λμ≠0，
≠
，
|λ（μ
）|=|λ||μ
|=|λ||μ||
|，|（λμ）
|=|λμ||
|=|λ||μ||
|，
即|λ（μ
）|=|（λμ）
|．若λ、μ同号，则等式两边都与
同向，若λ、μ异号，则等式两边都与
反向，
故 λ（μ
）与（λμ）
的模相同，方向相同，故这两个向量相等．
（2）若λ=0 或μ=0，或
=
，等式显然成立．若λμ≠0，
≠
，若λ和μ同号，
|（λ+μ）
|=|λ+μ||
|=（|λ|+|μ|）|
|，|λ
+μ
|=|λ
|+|μ
|=（|λ|+|μ|）|
|，
即|（λ+μ）
|=|λ
+μ
|，等式两边都与
同向，或都与
反向，故等式成立．
若λ和μ异号，当λ＞μ时，等式两边都与λ
同向，当λ＜μ时，等式两边都与λ
反向，
还可证明|（λ+μ）
|=|λ
+μ
|，故等式一定成立．
（3）当
，
中有一个等于零时，或λ=0或1时，等式显然成立．
当
，
都不等于0且λ≠1，λ≠0，
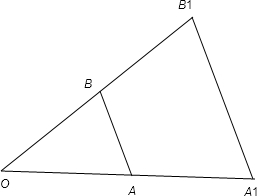
当λ＞0且λ≠1时，如图所示，设
=
，
=
，
=λ
，
=λ
，
则
=
+
，
=λ
+λ
，由作法知
∥
，∴|
|=λ|
|，
∴|
|=λ|
|，且
与
方向也相同，故有
=λ
，λ （
+
）=λ
+μ
成立．
当λ＜0时，同理可证．
综上，λ （
+
）=λ
+μ
成立．
故答案为 λ（μ
）=（λμ）
、（λ+μ）
=λ
+μ
、λ （
+
）=λ
+μ
．
| a |
| a |
| a |
| a |
| a |
| a |
| b |
| a |
| b |
证明：（1）若λ=0 或μ=0，或
| a |
| 0 |
| a |
| 0 |
|λ（μ
| a |
| a |
| a |
| a |
| a |
| a |
即|λ（μ
| a |
| a |
| a |
| a |
故 λ（μ
| a |
| a |
（2）若λ=0 或μ=0，或
| a |
| 0 |
| a |
| 0 |
|（λ+μ）
| a |
| a |
| a |
| a |
| a |
| a |
| a |
| a |
即|（λ+μ）
| a |
| a |
| a |
| a |
| a |
若λ和μ异号，当λ＞μ时，等式两边都与λ
| a |
| a |
还可证明|（λ+μ）
| a |
| a |
| a |
（3）当
| a |
| b |
当
| a |
| b |
当λ＞0且λ≠1时，如图所示，设
| OA |
| a |
| AB |
| b |
| OA1 |
| a |
| A1B1 |
| b |
则
| OB |
| a |
| b |
| OB1 |
| a |
| b |
| AB |
| A1B1 |
| A1B1 |
| AB |
∴|
| OB1 |
| OB |
| OB1 |
| OB |
| OB1 |
| OB |
| a |
| b |
| a |
| b |
当λ＜0时，同理可证．
综上，λ （
| a |
| b |
| a |
| b |
故答案为 λ（μ
| a |
| a |
| a |
| a |
| a |
| a |
| b |
| a |
| b |
点评：本题考查向量的数乘的定义及几何意义，体现了数形结合的数学思想．
练习册系列答案
相关题目
和
为直角坐标第xOy中与x轴和y轴正方向相同的单位向量，根据平面向量基本定理，对于该平面上的任意一个向量
，则存在唯一的一对实数λ，μ，使得
+μ
和
表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量，其中＜
，
和
为直角坐标第xOy中与x轴和y轴正方向相同的单位向量，根据平面向量基本定理，对于该平面上的任意一个向量
，则存在唯一的一对实数λ，μ，使得
=
+μ
，我们就把实数对（λ，μ）称作向量
的坐标．并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式．现在我们用
和
表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量，其中＜
，
＞=
，
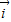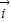和
做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量
的坐标；