题目内容
已知函数f(x)=log3
是奇函数,则a2012+2012a的值为( )
| 2-a+x |
| a-x |
| A.2013 | B.2012 | C.2011 | D.2010 |
当a=0时,f(x)=log3
不是奇函数
当a≠0时,若函数f(x)=log3
是奇函数,
则f(0)=log3
=0,
即
=1
解得a=1
∴a2012+2012a=1+2012=2013
故选A
| 2+x |
| -x |
当a≠0时,若函数f(x)=log3
| 2-a+x |
| a-x |
则f(0)=log3
| 2-a |
| a |
即
| 2-a |
| a |
解得a=1
∴a2012+2012a=1+2012=2013
故选A

练习册系列答案
相关题目
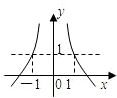
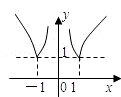
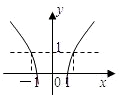
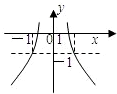
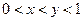 ,
,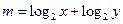 ,则有
,则有
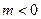 B
B 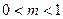 C
C 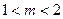 D
D