Question

如图，煤场的煤堆形如圆锥，设圆锥母线与底面所成的角为α．（α为常数）

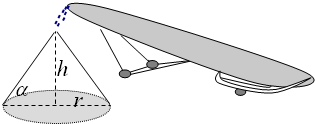
（1）高h与底面半径r有什么关系？
（2）传输带以0.3m³/min往煤场送煤形成新的煤堆，求当半径r=1.7m时的r对于时间t的变化率．
（参考数据：π取3.14，1.7²=2.89，1.7³≈4.91，为计算方便可取3.14×2.89≈9，3.14×4.91≈15）

Answer 1

分析：（1）由题意知，tanα=

h

r

，从而得出高h与底面半径r的关系．
（2）记tmin时煤堆的体积为V，写出圆锥的体积公式，求底面半径对于时间的变化率，即半径的函数式对于时间t求微分，代入所给的数据做出结果．

解答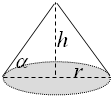：解：（1）由题意知，tanα=

h

r

，∴h=rtanα…（2分）
（2）记tmin时煤堆的体积为V，
则V=

1

3

πr2h=

1

3

πr3tanα=0.3t ①…（4分）
∴r=

3	0.9 πtanα

t

1

3

 ②…（5分）
②式两边对t求导，得r'（t）=

1

3

3	0.9 πtanα

t-

2

3

  ③…（7分）
（注：①式两边对t求导，同样可得，只不过是隐函数求导了，教师可以作此理解）
设r=1.7m时对应的时刻为t₀，由①得t₀=

πtanα

0.9

×1．73
∴

t

- 2 3 0

=(

πtanα

0.9

)-

2

3

×1．7-2…（10分）
代入③式得，
r'（t）=

1

3

3	0.9 πtanα

t0-

2

3

=

1

3

3	0.9 πtanα

•(

πtanα

0.9

)-

2

3

×1．7-2
=

0.3

πtanα

×1．7-2≈

0.3

9tanα

=

0.033

tanα

（m/min）…（15分）

点评：本题考查变化的快慢与变化率，本题解题的关键是注意求的是圆锥的底面半径对于时间的变化率．属于中档题．