题目内容
给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点,记O为坐标原点.(1)求
| OA |
| OB |
(2)设
| AF |
| FB |
| 5 |
分析:(1)根据抛物线方程可得焦点F的坐标,设出直线的方程与抛物线方程联立消去x,设A,B的坐标分别为(x1,y1)(x2,y2)根据韦达定理可求得y1y2进而求得x1x2的值进而可得答案.
(2)由
=λ
可知所以(1-x1,-y1)=λ(x2-1,y2),与抛物线方程联立整理得x1=λ2x2,进而求得y2和x2,代入三角形面积公式,进而根据面积的范围求得λ的范围.
(2)由
| AF |
| FB |
解答: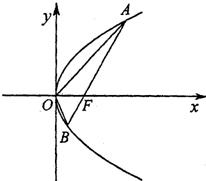 解:(1)根据抛物线方程y2=4x可得F(1,0)
解:(1)根据抛物线方程y2=4x可得F(1,0)
设直线l的方程为x=my+1,将其与C的方程联立,消去x得y2-4my-4=0
设A,B的坐标分别为(x1,y1)(x2,y2)
则y1y2=-4
因为
=4x1,
=4x2,所以x1x2=
=1
故
•
=x1x2+y1y2=-3
(2)解:因为
=λ
,
所以(1-x1,-y1)=λ(x2-1,y2)
即
又y12=4x1③y22=4x2④
由②、③、④消去y1,y2后得,x1=λ2x2
将其代入①,1-λ2x2=λx2-λ,整理后注意到λ>0,解得x2=
从而可得y2=-
,y1=2
故三角形OAB的面积S=
|OF|•|y1-y2|=
+
因为
+
≥2恒成立,所以只要解
+
≤
即可,
解得
≤λ≤
.
 解:(1)根据抛物线方程y2=4x可得F(1,0)
解:(1)根据抛物线方程y2=4x可得F(1,0)设直线l的方程为x=my+1,将其与C的方程联立,消去x得y2-4my-4=0
设A,B的坐标分别为(x1,y1)(x2,y2)
则y1y2=-4
因为
| y | 2 1 |
| y | 2 2 |
| 1 |
| 16 |
| y | 2 1 |
| y | 2 2 |
故
| OA |
| OB |
(2)解:因为
| AF |
| FB |
所以(1-x1,-y1)=λ(x2-1,y2)
即
|
又y12=4x1③y22=4x2④
由②、③、④消去y1,y2后得,x1=λ2x2
将其代入①,1-λ2x2=λx2-λ,整理后注意到λ>0,解得x2=
| 1 |
| λ |
从而可得y2=-
| 2 | ||
|
| λ |
故三角形OAB的面积S=
| 1 |
| 2 |
| λ |
| 1 | ||
|
因为
| λ |
| 1 | ||
|
| λ |
| 1 | ||
|
| 5 |
解得
3-
| ||
| 2 |
3+
| ||
| 2 |
点评:本题主要考查抛物线的应用.题中涉及向量的计算,不等式问题和解三角形等问题,综合性很强.

练习册系列答案
相关题目
给定抛物线C:y2=4x,F是其焦点,过F的直线l:y=k(x-1),它与C相交于A、B两点.如果
=λ
且λ∈[
,
].那么k的变化范围是( )
| FB |
| AF |
| 1 |
| 16 |
| 1 |
| 4 |
A、[
| ||||||||
B、[-
| ||||||||
C、[
| ||||||||
D、(-∞,-
|