题目内容
 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG,且AC=EF=1,AB=AD=DE=DG=2.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG,且AC=EF=1,AB=AD=DE=DG=2.(1)求证:平面BEF⊥平面DEFG;
(2)求证:BD∥平面ACGD;
(3)求三棱锥A-BCF的体积.
分析:(1)根据平面ABCD∥平面DEFG,证出AB∥DE.结合题意,得ADEB为平行四边形,所以BE∥AD.而AD⊥平面DEFG,得到BE⊥平面DEFG,从而证出平面BEF⊥平面DEFG.
(2)取DG的中点为M,连接AM、FM.结合题中位置关系和长度数据,证出AB∥FM且AB=FM,所以四边形ABFM是平行四边形,得BF∥AM,再结合线面平行的判定定理,可得BD∥平面ACGD.
(3)根据题意,易得F到面ABC的距离为AD.将三棱锥A-BCF的体积转化为三棱锥F-ABC的体积,计算出△ABC的面积,再结合锥体体积公式,不难求出三棱锥A-BCF的体积.
(2)取DG的中点为M,连接AM、FM.结合题中位置关系和长度数据,证出AB∥FM且AB=FM,所以四边形ABFM是平行四边形,得BF∥AM,再结合线面平行的判定定理,可得BD∥平面ACGD.
(3)根据题意,易得F到面ABC的距离为AD.将三棱锥A-BCF的体积转化为三棱锥F-ABC的体积,计算出△ABC的面积,再结合锥体体积公式,不难求出三棱锥A-BCF的体积.
解答: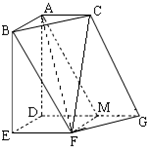 解:(1)∵平面ABCD∥平面DEFG,平面ABCD∩平面ADEB=AB,
解:(1)∵平面ABCD∥平面DEFG,平面ABCD∩平面ADEB=AB,
平面DEFG∩平面ADEB=DE
∴AB∥DE.
∵AB=DE,∴ADEB为平行四边形,得BE∥AD.…(2分)
∵AD⊥平面DEFG,∴BE⊥平面DEFG,
∵BE?平面BEF,
∴平面BEF⊥平面DEFG.…(4分)
(2)取DG的中点为M,连接AM、FM,则
∵EF∥DM,且EF=DM=1
∴四边形DEFM是平行四边形,
∴DE∥FM,DE=FM,
又∵DE∥AB,DE=AB,∴AB∥FM,AB=FM,…(6分)
∴四边形ABFM是平行四边形,得BF∥AM,
∵BF?平面ACGD,AM⊆平面ACGD,
∴BF∥平面ACGD.…(8分)
(3)∵平面ABCD∥平面DEFG,AD⊥平面DEFG,
∴F到面ABC的距离为AD.
由此可得三棱锥A-BCF的体积为
VA-BCF=VF-ABC=
•S△ABC•AD=
×(
×1×2)×2=
.…(12分)
 解:(1)∵平面ABCD∥平面DEFG,平面ABCD∩平面ADEB=AB,
解:(1)∵平面ABCD∥平面DEFG,平面ABCD∩平面ADEB=AB,平面DEFG∩平面ADEB=DE
∴AB∥DE.
∵AB=DE,∴ADEB为平行四边形,得BE∥AD.…(2分)
∵AD⊥平面DEFG,∴BE⊥平面DEFG,
∵BE?平面BEF,
∴平面BEF⊥平面DEFG.…(4分)
(2)取DG的中点为M,连接AM、FM,则
∵EF∥DM,且EF=DM=1
∴四边形DEFM是平行四边形,
∴DE∥FM,DE=FM,
又∵DE∥AB,DE=AB,∴AB∥FM,AB=FM,…(6分)
∴四边形ABFM是平行四边形,得BF∥AM,
∵BF?平面ACGD,AM⊆平面ACGD,
∴BF∥平面ACGD.…(8分)
(3)∵平面ABCD∥平面DEFG,AD⊥平面DEFG,
∴F到面ABC的距离为AD.
由此可得三棱锥A-BCF的体积为
VA-BCF=VF-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题给出特殊的六面体,求证线面平行、面面垂直并且求锥体体积.考查了线面垂直、线面平行的判定与性质和面面平行、面面垂直的判定与性质等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
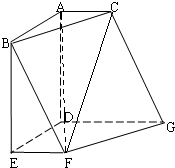 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG,且AC=EF=1,AB=AD=DE=DG=2.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG,且AC=EF=1,AB=AD=DE=DG=2.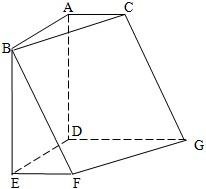 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.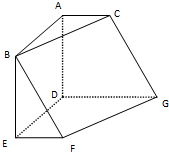 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,ED⊥DG,EF∥DG.且AC=EF=1,AB=AD=DE=DG=2.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,ED⊥DG,EF∥DG.且AC=EF=1,AB=AD=DE=DG=2.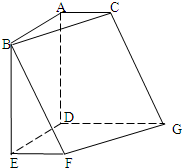 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.