题目内容
设数列 的前
的前 项和为
项和为 ,已知
,已知
(Ⅰ)求证:数列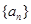 为等差数列,并写出
为等差数列,并写出 关于
关于 的表达式;
的表达式;
(Ⅱ)若数列 前
前 项和为
项和为 ,问满足
,问满足 的最小正整数
的最小正整数 是多少?
是多少?
【答案】
(Ⅰ)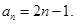 (Ⅱ)满足
(Ⅱ)满足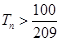 的最小正整数为12.
的最小正整数为12.
【解析】(I)由当 时,
时,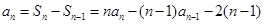 ,
,
得 .可知数列
.可知数列 是以
是以 为首项,2为公差的等差数列.
为首项,2为公差的等差数列.
(II) ,显然裂项求和的方法求和.
,显然裂项求和的方法求和.
解:(Ⅰ)当 时,
时,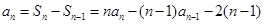 ,
,
得 .
.
所以数列 是以
是以 为首项,2为公差的等差数列. ……5分
为首项,2为公差的等差数列. ……5分
所以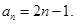 ……………………6分
……………………6分
(Ⅱ)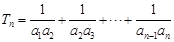

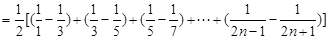

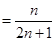 ……………10分
……………10分
由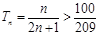 ,得
,得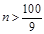 ,
,
满足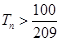 的最小正整数为12. …………………12分
的最小正整数为12. …………………12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的前
的前 项和为
项和为 ,已知
,已知 .
. ;
; 的前
的前 项和为
项和为 。已知
。已知 ,
, ,
, 。
。 ,求数列
,求数列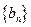 的通项公式;
的通项公式; ,
, 的取值范围。
的取值范围。