题目内容
已知P是椭圆
上一点，F1和F2是焦点，若∠F1PF2=30°，则△PF1F2的面积为（ ）A．
B．
C．4（2+
）D．4
【答案】分析：先根据椭圆的方程求得c，进而求得|F1F2|，设出|F1P|=x，|PF2|=y，利用余弦定理可求得xy的值，最后利用三角形面积公式求解．
解答：解：设|F1P|=x，|PF2|=y，c=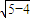
=1，
∴|F1F2|=2，
在△PF1F2中利用余弦定理可得cos30°=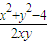
=
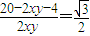
求得xy=16（2-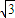
）
∴△PF1F2的面积为
×sin30°xy=4（2-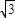
）
故选B
点评：本题主要考查了椭圆的简单性质．通过解三角形，利用边和角求得问题的答案．
解答：解：设|F1P|=x，|PF2|=y，c=
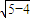=1，∴|F1F2|=2，
在△PF1F2中利用余弦定理可得cos30°=
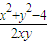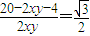
=求得xy=16（2-
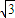）∴△PF1F2的面积为
×sin30°xy=4（2-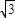）故选B
点评：本题主要考查了椭圆的简单性质．通过解三角形，利用边和角求得问题的答案．
练习册系列答案
相关题目
已知P是椭圆上一点，F是椭圆的一个焦点，则以线段PF为直径的圆和以椭圆长轴为直径的圆的位置关系是（ ）
| A、相离 | B、内切 | C、内含 | D、可以内切，也可以内含 |
上一点，F1、F2为椭圆两焦点，若∠F1PF2=90°，则ΔF1PF2的面积等于( )
上一点，F1和F2是焦点，若∠F1PF2=30°，则△PF1F2的面积为（ ）
）
上一点，F1和F2是焦点，若∠F1PF2=30°，则△PF1F2的面积为（ ）
）