题目内容
集合D={平面向量},定义在D上的映射f,满足对任意x∈D,均有f(x)=λx(λ∈R且λ≠0).
(1)若|a|=|b|,且a与b不共线,试证明:[f(a)-f(b)]⊥(a+b);
(2)若A(1,2),B(3,6),C(4,8),且f![]()
![]()
![]() =
=![]() ,求f(
,求f(![]() )·
)·![]() .
.
(1)证明:由题意有[f(a)-f(b)]·(a+b)=(λa-λb)(a+b)=λ(a2-b2)=0.∵f(a)-f(b)≠0,a+b≠0,∴[f(a)-f(b)]⊥(a+b).
(2)![]() =(2,4),
=(2,4),![]() =(1,2),∴f(
=(1,2),∴f(![]() )=λ(1,2)=(2,4),∴λ=2.又
)=λ(1,2)=(2,4),∴λ=2.又![]() =(3,6),∴f(
=(3,6),∴f(![]() )·
)·![]() =2(3,6)·(2,4)=60.
=2(3,6)·(2,4)=60.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
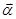 和
和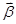 ,定义
,定义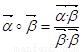 .若平面向量
.若平面向量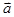 ,
,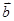 满足
满足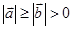 ,
,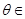
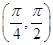 ,且
,且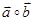 和
和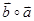 都在集合
都在集合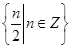 中,则
中,则 =( )
=( )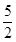 B.
B.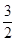 C.1 D.
C.1 D.