题目内容
在数列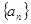 中,
中,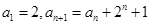
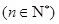 .
.
(Ⅰ)求证:数列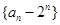 为等差数列;
为等差数列;
(Ⅱ)设数列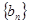 满足
满足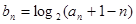 ,若
,若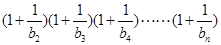
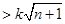 对一切
对一切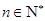 且
且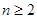 恒成立,求实数
恒成立,求实数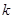 的取值范围
的取值范围
【答案】
解:(1)由 ,变形得:
,变形得: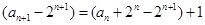
即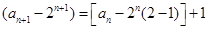 ,所以
,所以 ………………4分
………………4分
故数列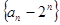 是以
是以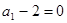 为首项,
为首项, 为公差的等差数列………………………5分
为公差的等差数列………………………5分
(2)由(1)得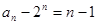 ,所以
,所以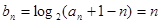 …………………………7分
…………………………7分
设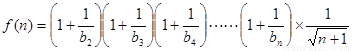
= =
= =
=
所以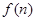 是关于
是关于 的单调递增函数,则
的单调递增函数,则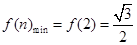
故实数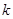 的取值范围是
的取值范围是
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目