题目内容
已知函数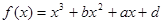 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为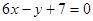 .
.
(Ⅰ)求函数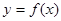 的解析式;
的解析式;
(Ⅱ)求函数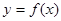 的单调区间.
的单调区间.
【答案】
(Ⅰ)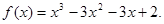 (Ⅱ)增区间是
(Ⅱ)增区间是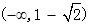 和
和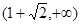 ,
,
减区间是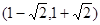 .
.
【解析】
试题分析:(Ⅰ)由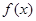 的图象经过P(0,2),知d=2,所以
的图象经过P(0,2),知d=2,所以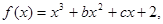
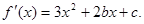
由在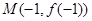 处的切线方程是
处的切线方程是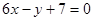 ,知
,知
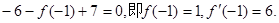
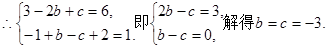
故所求的解析式是 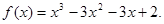 --------8分
--------8分
(Ⅱ)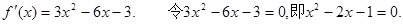
解得 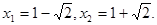 当
当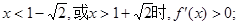
当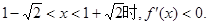
故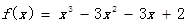 的增区间是
的增区间是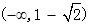 和
和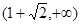 ,
,
减区间是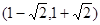 .
--------14分
.
--------14分
考点:导数的几何意义;利用导数研究函数的单调性。
点评:我们要灵活应用导数的几何意义求曲线的切线方程,尤其要注意切点这个特殊点,充分利用切点即在曲线方程上,又在切线方程上,切点处的导数等于切线的斜率这些条件列出方程组求解。属于基础题。

练习册系列答案
相关题目
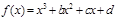 的图象过点P(0,2),且在点
的图象过点P(0,2),且在点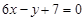 .求函数y=f(x)的解析式;
.求函数y=f(x)的解析式;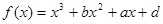 的图象过点P(0,2),且在点M
的图象过点P(0,2),且在点M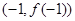 处的切线方程为
处的切线方程为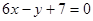 .
.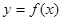 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数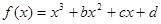 的图象过点P
的图象过点P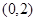 ,
且在点M
,
且在点M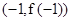 处的切线方程为
处的切线方程为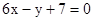 .
.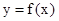 的解析式; (2) 求函数
的解析式; (2) 求函数