题目内容
下图为一几何体的展开图.(单位:cm)

(1)沿图中虚线将它们折叠起来,是哪一种特殊几何体?并请画出其直观图,比例尺是1∶2;
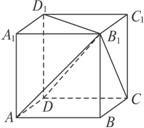
(2)需要多少个这样的几何体才能拼成一个棱长为6 cm的正方体ABCD—A1B1C1D1,请画出其示意图(需在示意图中分别表示出这种几何体);
(3)设正方体ABCD—A1B1C1D1的棱CC1的中点为E,试求:异面直线EB与AB1所成角的余弦值及平面AB1E与平面ABC所成二面角(锐角)的余弦值.
解:(1)折叠后是有一条侧棱垂直于底面的四棱锥,直观图如下.3分

(2)需要3个这样的几何体.5分
(3)①取DD1中点F,连结AF,则AF∥BE.
∴∠FAB1为异面直线EB与AB1所成的角.
易计算得 B1F=9,AF=3![]() ,AB1=6
,AB1=6![]() ,7分
,7分
∴cos∠FAB1=![]() =
=![]() =
=![]() .
.
∴异面直线EB与AB1所成角的余弦值为![]() .
.
②设B1E、BC的延长线交于点G,连结GA,则GA为平面AB1E与平面ABC所成二面角的棱,在底面ABC内作BH⊥AG,垂足为H.连结HB1,由三垂线定理知B1H⊥AG,
∴∠B1HB为平面AB1E与平面ABC所成二面角的平面角.
在Rt△ABG中,BH=![]() =
=![]() ,
,
∴HB1=![]() =
=![]() =
=![]() .
.
∴cos∠B1HB=![]() =
=![]() =
=![]() .
.
∴平面AB1E与平面ABC所成二面角的余弦值为![]() .
.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目

