题目内容
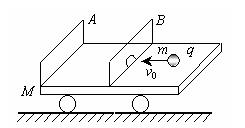
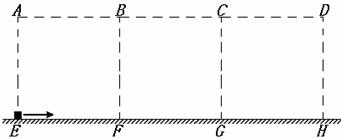
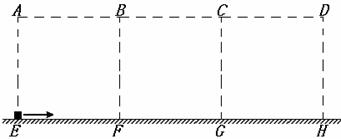
如图所示，绝缘的水平桌面上方有一竖直方向的矩形区域，该区域是由三个边长均为L的正方形区域ABFE、BCGF和CDHG首尾相接组成的，且矩形的下边EH与桌面相接。三个正方形区域中分别存在方向为竖直向下、竖直向上、竖直向上的匀强电场，其场强大小比例为1：1：2。现有一带正电的滑块以某一初速度从E点射入场区，初速度方向水平向右，滑块最终恰从D点射出场区，已知滑块在ABFE区域所受静电力和所受重力大小相等，桌面与滑块之间的滑动摩擦因素为0.125，重力加速度为g，滑块可以视作质点。求：
（1）滑块进入CDHG区域时的速度大小。
（2）滑块在ADHE区域运动的总时间。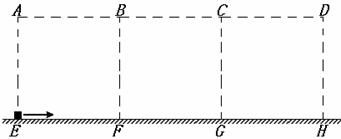
设三个区域的电场强度大小依次为E、E和2E，滑块在三个区域运动的时间分别为
、
和
：
（1）在CDHG区域，对滑块进行受力分析，由牛顿第二定律有 
而由题意知 
在水平方向和竖直方向分别有 
，
以上解得： 
，
（2）在BCGF区域，对滑块进行受力分析，在竖直方向
所以不受摩擦力，做匀速直线运动，
，
在ABFG区域，对滑块进行受力分析，在竖直方向 
在水平方向 
由滑动摩擦力定律： 
以上解得
当滑块由E运动到F时，由运动学公式 
代入解得
仍由运动学公式 
解得
所以
解析:
略
口算题卡加应用题集训系列答案
