题目内容
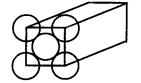
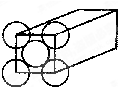金晶体是面心立方体，立方体的每个面5个金原子紧密堆砌（如图其余各面省略），金原子半径为1.44×10-10 m，求（1）金晶体中最小的一个立方体含有
4
4
个金属原子．（2）金的密度为
19.36
19.36
g?cm-3．（Au的原子量为197）分析：（1）利用均摊法计算每个晶胞中含有的金原子个数；
（2）每个金晶胞中含有4个原子，金晶体的边长a=
；再根据晶胞的边长计算其对角线长度，对角线长度就是金原子半径的4倍，半径已知，即可求出密度．
（2）每个金晶胞中含有4个原子，金晶体的边长a=
| 3 |
| ||
解答：解：（1）金晶胞是面心立方，所以每个金晶胞中含有的原子个数=8×
+6×
=4，
故答案为：4；
（2）每个金晶胞中含有4个原子，金晶体的边长a=
；对角线长度就是金原子半径的4倍，金原子半径为1.44×10-10 m=1.44×10-8 cm，再由晶胞的边长计算其对角线长度，
所以a2+a2=（4r）2，即（
）2+（
）2=（1.44×10-8）2，求出密度ρ=19.36g?cm-3，
故答案为：19.36．
| 1 |
| 8 |
| 1 |
| 2 |
故答案为：4；
（2）每个金晶胞中含有4个原子，金晶体的边长a=
| 3 |
| ||
所以a2+a2=（4r）2，即（
| 3 |
| ||
| 3 |
| ||
故答案为：19.36．
点评：本题考查晶胞的计算，明确晶胞体积与密度、相等原子质量的关系是解本题关键，难度较大，注意晶胞的边长不是金原子直径，为易错点．
练习册系列答案
相关题目
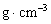。（用带A计算式表示）
。（用带A计算式表示）