题目内容
16.煤化工中常需研究不同温度下平衡常数、投料比及热值等问题.已知:CO(g)+H2O(g)?H2(g)+CO2(g)的平衡常数随温度的变化如下表:
| 温度/℃ | 400 | 500 | 800 |
| 平衡常数Kc | 9.94 | 9 | 1 |
(1)上述逆向反应是:放热 反应(选填:放热、吸热)
(2)在800℃发生反应,以表中的量投入恒容反应器,其中向正反应方向移动的有CDE.
| A | B | C | D | E | |
| n(CO2) | 3 | 1 | 0 | 1 | 1 |
| n(H2) | 2 | 1 | 0 | 1 | 2 |
| n(CO) | 1 | 0.5 | 3 | 2 | 3 |
| n(H2O) | 5 | 2 | 3 | 2 | 1 |
C(s)+CO2(g)?(g)平衡常数K;
C(s)+H2O(g)?(g)+H2(g)平衡常数K1;
CO(g)+H2O(g)?H2(g)+CO2(g) 平衡常数K2,则K、K1、K2之间的关系是:K=$\frac{K{\;}_{1}}{K{\;}_{2}}$.
(4)若在500℃时进行,若CO、H2O的起始浓度均为0.020mol/L,在该条件下,CO的最大转化率为75%.
(5)若在800℃进行,起始时CO和H2O(g)均为1mol,一段时间后反应达平衡,保持温度不变,继续向平衡体系中通入1molH2O(g),重新平衡时CO转化率为66.7%.
(6)在VL密闭容器中通入10molCO和10mol水蒸气,在T℃达到平衡,然后急速除去水蒸气(除水蒸气时各物质的物质的量不变),将混合气体燃烧,测得放出的热量为2842kJ(已知CO燃热为283kJ/mol,H2燃烧热为286kJ/mol),则T℃平衡常数K=$\frac{4}{9}$.
分析 (1)由表可知,温度越高,平衡常数越小,反应进行程度越小,平衡向逆反应移动,升高温度平衡向吸热方向移动;
(2)反应在同一容器内进行,体积相同,方程式中各物质的化学计量数都是1,所以在计算中均可用物质的量数值代替浓度数值,求出此时的浓度商Qc,平衡向正反应方向移动,浓度商小于平衡常数;
(3)根据化学平衡常数解答;
(4)到达平衡时转化率最大,令平衡时CO的浓度变化量为cmol/L,根据三段式法用c表示出平衡时各组分个浓度,再利用平衡常数列方程,求出c,再利用转化率定义计算;
(5)起始时水的物质的量为5xmol,转化的CO的物质的量为 5(1-x)ymol,利用三段式法求出平衡时各组分的物质的量,代入800℃平衡常数,据此解答;
(6)CO、H2的物质的量共为10mol,根据燃烧放出的热量求出CO、H2各自的物质的量,利用三段式法求出平衡时各组分的物质的量,代入平衡常数计算.
解答 解:(1)由表可知,温度越高,平衡常数越小,反应进行程度越小,平衡向逆反应移动,升高温度平衡向吸热方向移动,故正反应为放热反应,
故答案为:放热;
(2)反应在同一容器内进行,体积相同,方程式中各物质的化学计量数都是1,所以在计算中均可用物质的量数值代替浓度数值,800℃时反应平衡常数为1.
A、k=$\frac{c(H{\;}_{2})c(CO{\;}_{2})}{c(CO)c(H{\;}_{2}O)}$=$\frac{2×3}{1×5}$=$\frac{6}{5}$,大于1,反应向逆反应进行,故A错误;
B、k=$\frac{c(H{\;}_{2})c(CO{\;}_{2})}{c(CO)c(H{\;}_{2}O)}$=$\frac{1×1}{0.5×2}$=1,处于平衡状态,故B错误;
C、开始只有CO、H2,反应向正反应进行,故C正确;
D、k=$\frac{c(H{\;}_{2})c(CO{\;}_{2})}{c(CO)c(H{\;}_{2}O)}$=$\frac{1×1}{2×2}$=$\frac{1}{4}$,小于1,反应向正反应进行,故D正确;
E、k=$\frac{c(H{\;}_{2})c(CO{\;}_{2})}{c(CO)c(H{\;}_{2}O)}$=$\frac{2×1}{3×1}$=$\frac{2}{3}$,小于1,反应向正反应进行,故E正确;
故选:CDE;
(3)反应①C(s)+CO2(g)  2CO(g)平衡常数K=$\frac{{c}^{2}(CO)}{c(CO{\;}_{2})}$;
2CO(g)平衡常数K=$\frac{{c}^{2}(CO)}{c(CO{\;}_{2})}$;
反应②C(s)+H2O(g)  CO(g)+H2(g)平衡常数K1=$\frac{c({H}_{2})c(CO)}{c({H}_{2}O)}$;
CO(g)+H2(g)平衡常数K1=$\frac{c({H}_{2})c(CO)}{c({H}_{2}O)}$;
反应③CO(g)+H2O(g) H2(g)+CO2(g) 平衡常数K2=k=$\frac{c(H{\;}_{2})c(CO{\;}_{2})}{c(CO)c(H{\;}_{2}O)}$;
H2(g)+CO2(g) 平衡常数K2=k=$\frac{c(H{\;}_{2})c(CO{\;}_{2})}{c(CO)c(H{\;}_{2}O)}$;
反应②-反应③得反应①,所以K=$\frac{K{\;}_{1}}{K{\;}_{2}}$,
故答案为:K=$\frac{K{\;}_{1}}{K{\;}_{2}}$;
(4)令CO的浓度变化量为c,三段式法用c表示出平衡时各组分个浓度,
CO(g)+H2O(g)?H2(g)+CO2(g),
起始(mol/L):0.02 0.020 0 0
转化(mol/L):c c c c
平衡(mol/L):0.02-c 0.02-c c c
代入500℃时反应平衡常数有k=$\frac{c(H{\;}_{2})c(CO{\;}_{2})}{c(CO)c(H{\;}_{2}O)}$=$\frac{c×c}{(0.02-c)×(0.02-c)}$=9,解得c=0.015,
CO的最大所以转化率为 $\frac{0.015mol/L}{0.02mol/L}$×100%=75%,
故答案为:75%;
(5)因800℃时反应平衡常数为1,设CO转化的物质的量为x,
CO(g)+H2O(g)?H2(g)+CO2(g),
起始:1 2 0 0
转化:x x x x
平衡:1-x 2-x x x
因为反应中所有计量数都为1,且反应中容器体积不变,所以物质的量之比等于浓度之比,根据平衡常数k=$\frac{c(H{\;}_{2})c(CO{\;}_{2})}{c(CO)c(H{\;}_{2}O)}$=$\frac{x•x}{(1-x)•(2-x)}$=1,解得x=$\frac{2}{3}$,所以CO的所以转化率为 $\frac{\frac{2}{3}}{1}$×100%=66.7%,
故答案为:66.7%;
(6)由方程式CO(g)+H2O(g)=H2(g)+CO2(g)可知,有1molCO反应则生成1molH2,开始通入10molCO,所以平衡时,CO、H2的物质的量共为10mol.则平均燃烧热为 $\frac{2842kJ}{10mol}$=284.2kJ/mol,
利用十字交叉法计算CO、H2的物质的量之比,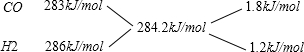
即CO、H2的物质的量之比为1.8kJ/mol:1.2kJ/mol=3:2,
所以n(CO)=10mol×$\frac{3}{5}$=6mol,n(H2)=10mol-6mol=4mol.
利用三段式法求出平衡时各组分的物质的量,
CO(g)+H2O(g)=H2(g)+CO2(g),
起始:10mol 10mol 0 0
转化:4mol 4 mol 4mol 4mol
平衡:6mol 6mol 4mol 4mol
所以常数平衡常数为k=$\frac{c(H{\;}_{2})c(CO{\;}_{2})}{c(CO)c(H{\;}_{2}O)}$=$\frac{4×4}{6×6}$=$\frac{4}{9}$,
故答案为:$\frac{4}{9}$.
点评 本题主要考查平衡常数及其计算,难度较大,注意(1)平衡常数书写,(2)平衡常数只受温度影响,同一反应温度不变,平衡常数不变.

| A. | 稀豆浆--胶体 | B. | 碳酸钠--正盐 | ||
| C. | 铜--非电解质 | D. | NaH+H2O=NaOH+H2↑--氧化还原反应 |
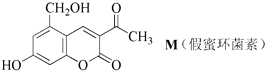
| A. | 1molM最多可和1molNa2CO3发生反应 | |
| B. | 1molM最多可和6molH2发生加成反应 | |
| C. | 1molM最多可和3molNaOH反应 | |
| D. | 1molM最多可和2molNa反应 |
| A. | Mg+2HCl═MgCl2+H2↑ | B. | 2NO+O2═2NO2 | ||
| C. | CuO+H2$\frac{\underline{\;\;△\;\;}}{\;}$Cu+H2O | D. | CaCl2+Na2CO3═CaCO3↓+2NaCl |





 .
. .
.